Escrever a Tag aqui (nome do capítulo IGUALZINHO), Outra tag, Mais uma tag
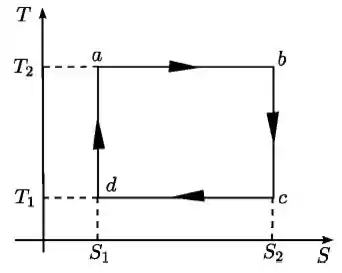
Seja o ciclo abaixo, realizado por n moles de um gás ideal, no plano . Considere conhecidas as temperaturas e e a diferença de entropia
- Calcule o calor transferido em cada etapa ( em função de , , indicando se este foi absorvido pelo sistema ou cedido pelo mesmo.
- Calcule a diferença de energia interna em cada etapa ( em função de , onde é a capacidade térmica molar a volume constante do gás.
- Calcule o trabalho total do ciclo, em função de , indicando claramente se este foi realizado pelo sistema ou sobre ele.
- Este ciclo representa uma máquina ou um refrigerador? Justifique. Se você achar que representa uma máquina, calcule a sua eficiência térmica Se você achar que é um refrigerador, calcule o coeficiente de desempenho
Passo 1
a)
Aqui basta a gente lembrar que:
E então é so aplicar a cada trecho.
Passo 2
Trechos:
Aqui a temperatura é constante, então:
É maior que zero porque a variação de entropia é positiva.
Nesse trecho, a entropia é constante, assim, a variação de entropia é nula o que nos leva a:
Assim, não há troca de calor nesse trecho. O trecho é uma transformação adiabática.
Passo 3
Nesse trecho a temperatura também é constante, então fazemos como em
Menor que zero já que a variação de entropia é negativa.
Que nem o trecho
Passo 4
b)
Basta a gente aplicar a fórmula pra cada trecho, prestando atenção quando a temperatura for constante:
Assim:
Passo 5
c)
Para um ciclo, temos que a variação de energia interna é nula. Assim:
Então basta a gente calcular o calor total do ciclo:
Já que:
Passo 6
d)
Representa uma máquina térmica, já que o trabalho do ciclo é positivo. Assim:
O calor é absorvido onde ele é positivo, assim:
Assim:
Resposta
a)
b)
c):
d):
Máquina térmica