Suponha que () de um gás diatômico ideal () opera em uma máquina de Carnot entre as temperaturas de e . A pressão em é 6. Na expansão isotérmica o volume é duplicado.
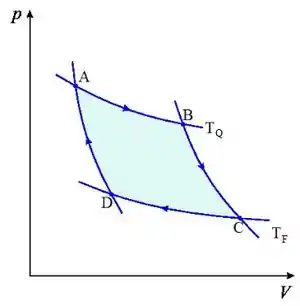
Dados: AB e CD são isotermas, BC e DA são adiabáticas.
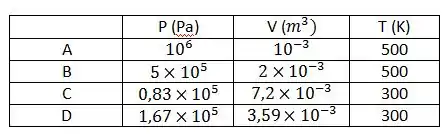
a) Calcule a pressão e o volume nos pontos A, B, C e D do diagrama PV da figura.
b) Calcule o calor, o trabalho e a transformação de energia interna para cada transformação do ciclo.
c) Calcule a eficiência da máquina.
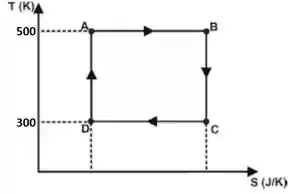
d) Calcule a variação de entropia em cada transformação do ciclo e represente o ciclo num diagrama T S (temperatura do gás em função da entropia) identificando os estados térmicos A, B, C e D.
Passo 1
a) No processo :
É um processo isotérmico! Então . E o problema disse que na expansão isotérmica o gás dobra de volume. Então .
Vamos calcular o volume em A:
Como é uma isoterma, podemos escrever:
Passo 2
No processo teremos uma adiabática. Em processos adiabáticos podemos escrever:
Com como dado no enunciado. Então:
Vou escrever isso de outro jeito:
No ponto C a gente também pode fazer:
Trocando na relação que a gente achou:
E vai ser:
Passo 3
Para calcular a pressão e o volume no ponto D usaremos o processo em vez do .
No processo temos uma adiabática! Vai valer a relação:
Substituindo os valores de A:
Mas a gente consegue achar :
Então:
E a pressão vai ser:
Colocando na tabela:
Passo 4
Passo 5
b) No processo
É uma isoterma, então a variação de energia interna é zero!
Pela primeira lei da termodinâmica:
E o trabalho a gente calcula:
Passo 6
No processo :
É um processo adiabático, então:
Pela primeira lei da termodinâmica:
Podemos calcular a energia interna pela fórmula:
Em que g é o número de graus de liberdade. Como é um gás diatômico, g = 5. Então:
Passo 7
No processo :
É uma isoterma, então a variação de energia interna é zero de novo.
Pela primeira lei da termodinâmica:
E o trabalho a gente calcula, de novo:
Passo 8
No processo :
É um processo adiabático, então:
Pela primeira lei da termodinâmica:
Podemos calcular a energia interna pela fórmula:
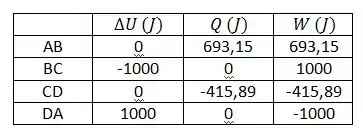
Fazendo a tabelinha:
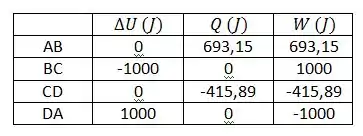
Passo 9
c) Como é uma máquina de Carnot podemos calcular:
Passo 10
d) A entropia é:
Nos processos adiabáticos, então, vai ser zero. Porque Q é igual a zero nesses processos.
Passo 11
Nos processo isotérmicos:
Então:
E:
Passo 12
Como nos processos e a entropia não varia, esses processos serão retas verticais no gráfico T S. Como nos processos e a temperatura não varia, serão retas horizontais no gráfico T S.
Vai ficar assim:
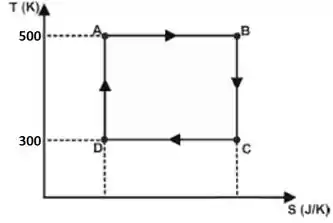
Resposta
a)
b)
c)
d) , e