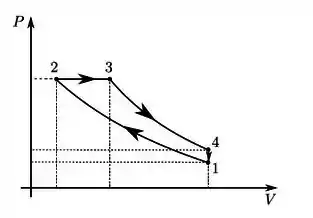
Considere o ciclo diesel reversível, formado por uma isóbara, uma isócora e duas adiabáticas, realizado por um mol de gás ideal, como representado no diagrama P-V abaixo:
a) Calcule o trabalho total no ciclo, em termos das temperaturas nos estados 1, 2, 3 e 4 e da capacidade térmica molar a volume constante do gás.
b) Calcule o rendimento do ciclo, em termos das temperaturas nos estados 1, 2, 3 e 4 e da razão entre as capacidades térmicas molares à pressão e volume constantes.
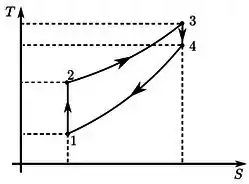
c) Represente o ciclo no diagrama S-T, indicando claramente qual o comportamento em cada etapa.
Passo 1
a) Primeiro vamos identificar as curvas! O problema disse pra gente que são: uma isócora (volume constante), uma isóbara (pressão constante), e duas adiabáticas (sem troca de calor).
Vamos começar pelo mais fácil de identificar. Em qual das curvas o volume não varia? Na curva , porque é uma linha vertical!
Em qual das curvas a pressão não varia? Na curva , porque é uma linha horizontal. Nessa linha o volume aumenta, então é uma expansão isobárica.
As outras duas curvas serão as adiabáticas, sendo que: ocorre compressão (o volume diminui) e ocorre expansão (o volume aumenta). Então:
- Curva (12): compressão adiabática.
- Curva (23): expansão isobárica.
- Curva (34): expansão adiabática.
- Curva (41): isócora.
- Curva (12): compressão adiabática.
- Curva (23): expansão isobárica.
- Curva (34): expansão adiabática.
- Curva (41): isócora.
Passo 2
No primeiro item ele pergunta o trabalho total no ciclo. Aí nós vamos ter que usar a Lei da Termodinâmica! Que é essa aqui:
Em que:
A variação de energia interna vai ser igual a zero no ciclo. Então:
Se acharmos então achamos o trabalho.
Passo 3
Agora pensa aqui comigo. Nós teremos duas adiabáticas. Nessas curvas o sistema não recebe nem cede calor! Então o calor vai ter que ser cedido e recebido nas outras curvas. Em qual curva você acha que o sistema cede calor e em qual ele recebe?
Na curva ele recebe calor, porque aumenta de volume. Na curva ele cede calor, porque a pressão diminui a um volume constante. Então:
Como essas duas curvas são de pressão e volume constante, nós podemos calcular usando a capacidade térmica:
Lembrando que :
Vamos substituir:
Então:
Passo 4
b) No segundo item ele pede o rendimento do ciclo. Esse rendimento pode ser calculado:
Em que .
Vamos substituir o que já temos:
Isso vai dar:
Passo 4
c) Nas duas curvas adiabáticas, não haverá variação de entropia! Então no diagrama S-T, esses processos serão representados por duas retas verticais.
No processo 12, como é uma compressão, a temperatura vai aumentar. No processo 34, como é uma expansão, a temperatura vai diminuir.
Vamos lembrar que a Entropia no processo pode ser calculada:
Na expansão isobárica:
Mas, a pressão constante, podemos escrever a primeira lei desse jeito aqui ó:
Porque .
E derivando:
Então:
Passo 5
Ok, agora vamos por partes como Jack, O Estripador.
Porque:
E:
Porque:
Show. Substituindo então:
Caramba, mas nós não sabemos quem são e . Vamos tentar descobrir? Acompanha comigo:
Vamos isolar os caras constantes:
Lembrando que no processo de 2 a 3 a pressão é constante!
Ok, vamos trocar.
Trocando por :
UFA!
Passo 6
Nós vamos fazer a mesma coisa pra curva isocórica. Mas calma que vai ser um pouquinho mais fácil.
Como o volume é constante, vai ser zero.
No mesmo esquema:
Passo 7
Na hora de construir o gráfico: o macete é começar pelas verticais! As duas verticais serão as adiabáticas: 12 e 34. Qual você acha que vai ter mais entropia? Vai ser a reta 34, porque no processo de 2 a 3 o gás recebe calor. Então:
A primeira reta terá os pontos 1 e 2 e a segunda reta os pontos 3 e 4.
Vamos analisar as temperaturas agora:
A temperatura aumenta porque o sistema foi comprimido sem perder calor.
A temperatura aumenta de novo porque o sistema recebe calor.
A temperatura diminui porque o sistema aumenta de volume sem receber calor.
A temperatura diminui porque a pressão diminui a volume constante.
Colocando no gráfico e cruzando as linhas:
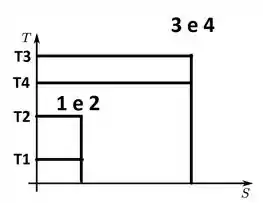
Vai ficar mais ou menos assim:
Resposta
a)
b)
c)