Um mol de um gás ideal é submetido a um ciclo reversível consistindo de duas ADIABÁTICAS e duas ISÓCORAS, como mostra o diagrama - na figura.
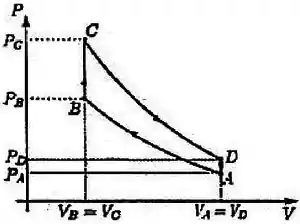
Marque a opção que melhor representa o MESMO ciclo em um diagrama -.
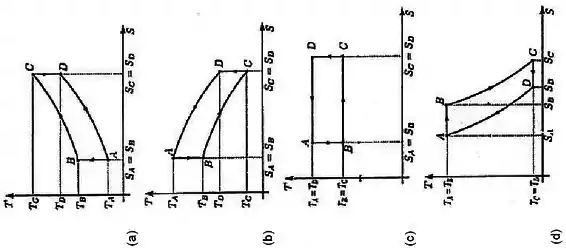
Passo 1
O primeiro passo para transformar um diagrama - em - é conferir se tem alguma isoterma ou adiabática, porque no diagrama - essas transformações são retas.
Nesse caso, temos duas transformações adiabáticas.
Pela figura, as adiabáticas são e .
Transformações adiabáticas são retas verticais no diagrama -, pois a entropia é constante.
Observação: lembrando que processos adiabáticos e reversíveis tem entropia constante:
Pelas alternativas, podemos eliminar a letra .
Passo 2
Agora que sabemos que temos duas adiabáticas, temos que ver o sentido.
Primeiro: no diagrama - mostrado, o sentido do ciclo é horário.
Como o trabalho é a área do ciclo nos dois diagramas, então o sentido do ciclo no diagrama - também deve ser horário.
Observação: lembrando que o sentido do ciclo determina se o trabalho é positivo ou negativo. Se for sentido horário, é positivo e vice-versa.
Assim, podemos eliminar as letras e .
Logo, só nos resta a letra como resposta.
Passo 3
Só para garantir que esta é a resposta certa, podemos ver que nos processos isovolumétricos, a pressão aumenta.
Aplicando a equação dos gases ideais no processo , por exemplo:
Como :
Como , então .
De fato, podemos observar isso na resposta da letra !
Resposta
Alternativa .