Uma máquina térmica usa, como fluido de trabalho, dois moles de um gás ideal diatômico, cuja capacidade térmica molar vale . O gás é submetido aos seguintes processos reversíveis:
Uma compressão adiabática, partindo de uma temperatura e de um volume , até que seu volume se reduza a metade, no estado .
Uma expansão isotérmica, do estado até o estado , onde seu volume retorna ao valor inicial.
( Um resfriamento isocórico, até que sua temperatura volte ao valor inicial, fechando assim o ciclo.
- Determine temperatura do gás no estado .
- Determine o calor transferido ao gás em cada uma das etapas.
- Determine a variação da entropia do gás em cada uma das etapas.
- Dado que o valor da entropia no estado vale , faça um esboço deste ciclo num diagrama , deixando claro cada uma das etapas.
Atenção: Deixe suas respostas em termos de e . Se achar conveniente, use que
Passo 1
Para um processo adiabático num gás ideal, temos que:
Onde
Então,
Sabemos que , logo:
Passo 2
Vamos analisar o calor em cada uma das etapas do ciclo .
Processo adiabático, logo .
Como se trata de um processo isotérmico em que não há variação de temperatura, temos que . Logo,
: Temos um processo a volume constante em que .
Passo 3
A variação de entropia é dada pela seguinte expressão:
Sabendo isso, vamos analisar a entropia para cada trecho do ciclo.
Como se trata de um processo adiabático, temos que:
Logo,
, processo isentrópico.
Na expansão isotérmica,
: Temos um processo isocórico em que:
Logo, substituindo da expressão da entropia, temos:
Nesse processo a temperatura é mantida constante, portanto podemos afirmar que
Passo 4
O processo é uma compressão adiabática reversível. Ou seja, o processo é isentrópico (sem variação de entropia). Em outras palavras, a entropia do estado é igual à entropia do estado .
Então no diagrama será uma reta vertical (se colocarmos no eixo vertical temperatura e no horizontal entropia), onde a temperatura irá aumentar, já que . Usando a aproximação , passa a valer:
O processo é uma expansão isotérmica onde a entropia do gás vai aumentar, já que num processo isotérmico e por ser uma expansão. Como é um processo isotérmico, .
Já a entropia do estado será a entropia do estado mais a variação de entropia entre os estados e .
Usando a aproximação :
Depois, basta ligar com e correr para o abraço!
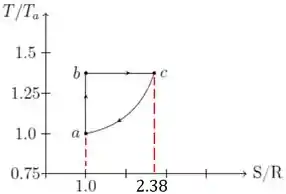
Resposta
a)
b) ;
;
: :
c) ;
;
: :
d)