Considere um feixe de luz monocromática, com comprimento de onda conhecido, que incide perpendicularmente num conjunto de fendas cuja estrutura queremos descobrir.
Após passar pelas fendas, a luz incide uma placa fotográfica paralela às fendas que registra uma série de traços claros (máximos) e escuros (mínimos) como mostrado na figura abaixo.

Esta figura foi interpretada como tendo uma intensidade relativa dada pela figura seguinte, onde na região entre e foram medidos 17 picos luminosos.
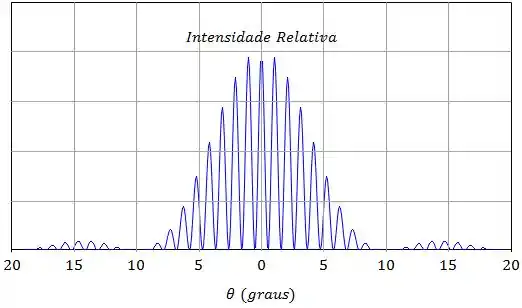
Considere que nos dois pontos referentes a a intensidade relativa é nula e que e que . Simplifique o máximo possível o seu resultado.
Quantas fendas existem no conjunto? Com base nos dados experimentais as fendas são pontuais? Há uma separação entre elas?
Se as fendas não forem pontuais, qual sua largura?
Qual a separação entre as fendas?
Qual a intensidade relativa do terceiro pico (sem contar o pico central) à direita do pico central, sabendo que o pico central tem intensidade máxima igual a ?
Passo 1
Quantas fendas existem no conjunto? Com base nos dados experimentais as fendas são pontuais? Há uma separação entre elas?
Para interferência com fendas, sabemos que entre dois máximos principais, existem máximos secundários.
No gráfico de intensidade, não temos nenhum máximo secundário entre dois máximos principais, logo:
Passo 2
Caso as fendas fossem pontuais, os máximos principais teriam a mesma amplitude. No gráfico de interferência, podemos ver que, a partir do máximo central, conforme aumenta ou diminui, as amplitudes dos máximos principais decaem.
Esse comportamento é típico de difração. Logo, as fendas não são pontuais.
Portanto, as duas fendas possuem uma abertura e um espaçamento entre elas.
Passo 3
Se as fendas não forem pontuais, qual sua largura?
A intensidade relativa é dada por:
Onde:
Onde o termo está relacionado à difração (é só observar que é na expressão de que aparece a largura das fendas).
O enunciado diz que em a intensidade relativa é nula. Assim, o primeiro mínimo de difração se dará quando:
Segundo o enunciado, . Logo:
Passo 4
Qual a separação entre as fendas?
Se quisermos calcular a separação entre as fendas, temos que olhar pros efeitos de interferência entre as fendas.
Olhando para a equação da intensidade relativa
Onde:
O termo está relacionado com a interferência (é só observar que é na expressão de que aparece a separação entre as fendas).
Os máximos de interferência no gráfico de intensidade acontecem quando:
Logo:
Substituindo a expressão de , teremos:
Como já esperávamos porque, quando falamos em interferência, os máximos de interferência são dados por:
Agora precisamos de um valor para .
Passo 5
Bom, o problema nos diz que na região entre e foram medidos 17 picos luminosos.
Como são 17 picos luminosos, eles estarão associados aos seguintes valores de :
Entretanto, os picos e aparecem antes do mínimo de difração, em .
Assim, o máximo valor de corresponderá ao máximo de interferência que coincide com o primeiro mínimo de difração .
Isso acontece porque, se um máximo de interferência coincide com o mínimo de difração, nós continuaremos não vendo esse pico luminoso, que estaria .
Por isso vemos apenas 17 picos luminosos (1 no centro, 8 à esquerda e 8 à direita) e não vemos os dois picos luminosos presentes no ângulo à esquerda e à direita.
Esses picos luminosos correspondem a . Logo, o máximo valor de é 9.
Sendo assim:
Onde e .
Passo 6
Qual a intensidade relativa do terceiro pico (sem contar o pico central) à direita do pico central, sabendo que o pico central tem intensidade máxima igual a ?
A intensidade relativa é dada por:
Onde:
O terceiro pico luminoso corresponderá a , logo:
Substituindo as expressões de , e , teremos:
Obs: Já escrevi os coeficientes e divididos por dois pois é assim que eles aparecem na fórmula da intensidade relativa.
Passo 7
Agora já podemos calcular a intensidade:
Onde:
Logo:
Resposta
Há duas fendas no conjunto. Ambas as fendas possuem uma abertura e um espaçamento entre elas.