Uma placa opaca tem algumas fendas igualmente espaçadas de uma distância de . A abertura de cada fenda é de . A placa é iluminada perpendicularmente por uma luz amarela com comprimento de onda . Em uma tela distante de da placa, a intensidade da luz é observada (ver figura).

(b) Faça um esboço qualitativo da intensidade da luz na tela em função do ângulo θ, evidenciando os máximos principais de interferência contidos dentro do máximo central e primeiro máximo secundário de difração.

Sabemos que as duas fórmulas principais que temos para esse tipo de situação é dada pelo mínimo de difração e pelo máximo de interferência, sabemos que as duas formula são

Interferência

Difração

Se dividirmos uma fórmula pela outra teremos que

Simplificando teremos que

No enunciado nos foi dado o valor de d e de a, substituindo teremos que

Isso significa que quando

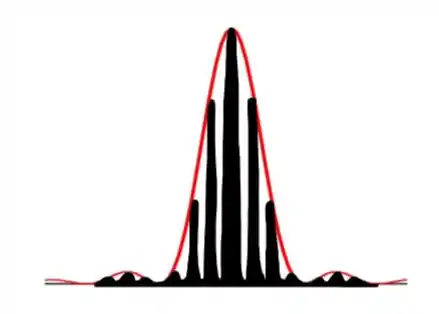
Isso pode ser analisado da seguinte maneira, dentro da envoltória central de difração, temos exatamente 3 máximos de interferência (lembrando que estamos analisando apenas a parte positiva, como também temos a parte negativa da envoltória, significa que teremos ainda mais 3 máximos de interferência na parte de baixo da figura). Lembrando que concluímos ser 3 máximos de interferência pois a nossa relação é de 3,5, ou seja, o numero de valores inteiros entre 0 e 3,5 é exatamente de 3.

Para fazermos a contabilização do número de máximos de interferência basta fazermos

Na envoltória seguinte faremos o mesmo processo, mas agora começando por m=4, e indo até m=6, ou seja, mais 3 máximos de interferência, e devemos tomar um cuidado aqui, pois em m=7 teremos uma coincidência entre o mínimo de difração e o máximo de interferência, isso é fácil de analisar pois 7 é múltiplo de 3,5 que é exatamente a nossa relação entre interferência e difração dado por .

Agora só falta esboçarmos o gráfico, mas tomaremos o cuidado de ignorar os máximos secundários de interferência, que aparecem para N>2, com isso nosso gráfico será