Um feixe de luz monocromática de frequência natural ilumina coerentemente um anteparo opaco com 3 fendas idênticas de largura , e igualmente espaçadas de .
Observa-se a figura de interferência em um anteparo distante de das fendas. Determine:
- A distância entre mínimos de interferência. Deixe claro quais foram os mínimos escolhidos.
- A distância entre máximos principais de interferência. Deixe claro quais foram os máximos escolhidos.
- Determine o valor da largura tal que o 1° mínimo de difração anule o 3° máximo de interferência.
- Utilizando o valor da largura do item “(c)”, quantas franjas brilhantes existem dentro do máximo central da difração?
Passo 1
O mais importante aqui é observar que estamos em um problema de difração em fendas, onde , pois o problema menciona 3 fendas e menciona suas larguras.
Letra a)
Entre pares de máximos principais sucessivos temos mínimos, dados por:
Onde é um número inteiro que não seja múltiplo de .
No nosso caso, , e assim:
Sendo que é a diferença de fase devido a distância entre as fendas.
Antes de irmos pro próximo passo, um comentário rápido. Como comentei, é um número inteiro qualquer, e por isso estamos considerando TODOS os mínimos.
Mas tem uma segunda forma de pensar. Seja o máximo de ordem e o máximo de ordem . Os mínimos entre eles vão ser dados por:
Onde apenas neste caso. Essa equação deixa mais claro aonde estamos na figura de difração por 3 fendas, mas é equivalente ao que conversamos antes.
Rearrumando:
E nesse caso, , voltando pra nossa equação.
Os dois primeiros mínimos estão entre e 1 (o máximo central e o primeiro logo depois), e logo correspondem a:
Os mínimos seguintes correspondem a , e assim:
E por aí vai, no nosso caso sendo:
Passo 2
Para ver então a distância do mínimo até o centro da figura, podemos usar a tangente do ângulo.
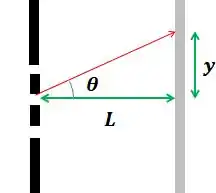
Usando a aproximação de pequenos ângulos, temos que .
Escolhendo o primeiro mínimo () e o segundo mínimo (), a distância entre eles vai ser:
Pelo enunciado, nós temos que e . Mas não temos , apenas a frequência.
Mas isso é suficiente pra achar , pois:
Sendo a frequência e . Substituindo tudo:
Passo 3
Letra b)
Para saber a distância entre dois máximos principais, precisamos saber suas posições, que são dadas por:
Usando o mesmo triângulo de antes, temos:
A distância entre os máximos de ordem e vai ser:
Passo 4
Letra c)
O primeiro mínimo de difração corresponde a
O terceiro máximo de interferência corresponde a
Para um anular o outro, essas equações devem ser iguais.
Passo 5
Letra d)
Como o primeiro mínimo de difração elimina a terceira franja brilhante principal, nós temos 2 franjas brilhantes principais de cada um dos lados da franja brilhante central.
Temos então 5 franjas brilhantes principais no máximo central de difração.
Porém, entre cada par de franjas principais consecutivas, temos franjas brilhantes secundárias. Esses pares são:
e
e
Temos 6 pares de franjas principais consecutivas, correspondendo a 6 franjas secundárias.
Somando tudo, temos:
A figura ficaria da seguinte forma:
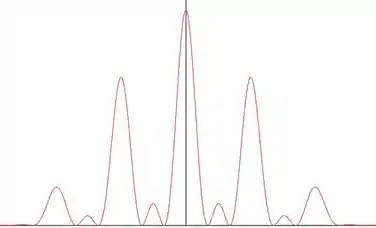
Têm dois máximos secundários que são muito difíceis de ver, que estão nas laterais dessa parte da envoltória (os extremos à esquerda e à direita).
Essa dificuldade é devido à sua proximidade dos mínimos de difração.
Resposta
Letra a)
Escolhendo os mínimos de ordens e , temos:
Letra b)
Escolhendo os máximos principais de ordens e , temos:
Letra c)
Letra d)