Exercícios Resolvidos de Distância entre Planos

Enunciado

(b) A equação cartesiana do plano é da forma:

Onde a, b e c são as coordenadas de um vetor normal ao plano e o coeficiente d achamos substituindo um ponto que pertence ao plano nessa equação.

Queremos um plano que contenha os pontos A, B e C.

Vamos usar os vetores do plano:

Se fizermos o produto vetorial entre esses dois caras, vamos obter um vetor que é ortogonal a eles, e, portanto, ortogonal (normal) ao plano!

Vamos achar esse vetor então:

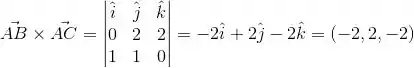
Podemos dividir o vetor por 2 e ainda vamos ter um vetor normal de coordenadas:

Então substituindo por a equação do plano fica:

Agora substituímos as coordenadas do ponto nessa equação e achamos d:

Então a equação cartesiana do plano que buscamos é:

É paralelo ao plano que achamos antes, porque esse coeficiente d faz com que o plano seja transladado.

Mas sabemos que a distância entre os planos tem que ser 1.

Lembra como faz para achar a distância entre dois planos??

A gente escolhe um ponto que pertence a um dos planos e depois usamos a formulazinha:

Pra achar a distância desse ponto ao outro plano!

Então vamos escolher o ponto que pertence ao plano (poderia ser qualquer outro) e aplicar a fórmula de distância com relação ao plano de equação .

Fazendo isso:

Mas queremos que a distância seja igual a 1, então:

Temos então duas possibilidades:

Aí já temos as equações dos dois planos pedidos no enunciado:

(b)