Considere o tetraedro onde , , e .
a) Ache uma equação para o plano que contém os pontos , e .
b) Calcule a distância de a .
c) Determine a medida angular entre o plano e a reta que passa por e .
d) Determine uma equação geral para cada plano que é paralelo ao plano e dista dele. Qual destes planos intercepta o tetraedro?
Passo 1
a) Esse plano terá como vetores diretores e .
Então, podemos dizer que um vetor normal do plano será o produto vetorial de e fechou?
Passo 2
Então bora calcular o produto vetorial :
Fechou, o vetor normal do plano é , então a equação dele vai ser assim:
Agora temos que substituir um ponto do plano nessa equação para encontrarmos o valor de ok?
Passo 3
Substituindo o ponto na equação (mas também poderia ser ou ):
Ou seja, a equação do plano é
Passo 4
b) Relembrando a fórmula da distância entre ponto e plano:
Beleza, bora substituir os valores:
Então a distância entre o plano e o ponto é:
Passo 5
c) A reta que passa por e vai ter vetor diretor . Pra calcular o ângulo entre essa reta e o plano , basta calcularmos o ângulo entre e o vetor normal de utilizando produto escalar:
Então o ângulo entre a reta e o plano vai ser:
Passo 6
d) Só vão existir 2 planos que satisfaçam essas condições: um vai estar “na frente” de e o outro vai estar “atrás”. Ambos são paralelos a ele e têm uma distância de de certo?
Bom, primeiramente, se eles são paralelos a , o seu vetor normal também vai ser , logo, a equação geral dos dois vai ser nesse estilo aqui:
E novamente precisamos descobrir esse tal desse que satisfaça o que queremos ok?
Passo 7
Para encontrarmos a equação completa do plano, precisamos achar um ponto em cada um dos planos que tenha uma distância de até . Igualando a fórmula da distância entre ponto e plano a :
Como temos um módulo ali, vamos chegar nas duas possíveis respostas:
Boaaa, encontramos nossos 2 planos :D
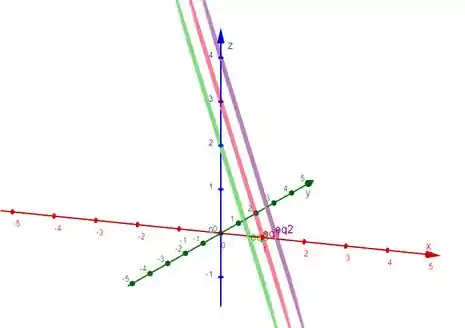
Na imagem acima temos em verde o plano , em vermelho o plano e em roxo o plano , vistos lateralmente ;)
Passo 8
Para encontrarmos qual dos 2 planos intercepta o tetraedro, vamos verificar qual deles tem a menor distância até o ponto .
Isso porque lembra que o plano contem os pontos , e , certo? E esses pontos nós vamos ver como a base do tetraedro.
Então o tetraedro vai “em direção” ou ao plano ou ao plano . Olha o desenho ali no passo anterior pra ficar mais claro hehe
Resumindo: o ponto é o “pico” desse tetraedro. Então o plano que estiver mais próximo de é o plano que passa pelo tetraedro.
Passo 9
Substituindo e na equação da distância entre ponto e plano:
Como , ou seja, como o plano está mais próximo do ponto do que , então é o plano que intercepta o tetraedro :)
Observe abaixo com os devidos pontos do tetraedro.
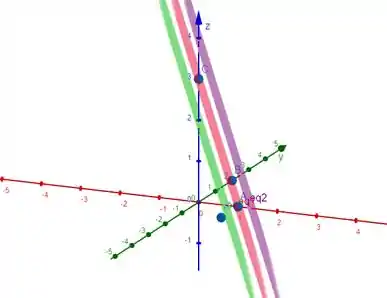
Resposta
a)
b)
c)
d)
(esse intercepta o tetraedro)