Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Distância entre Planos

Ver Teoria
Exercício 2134567

Enunciado

Considere as reta r e l dadas por: r : x = 0 ,   y = 2 + t e z = 1 + t ; l : x - 2 = z + 1 e y = 3 ;

  1. Mostre que r e l são reversas
  2. Encontre os planos π e α tais que: r ⊂ π ,   l ⊂ α e π é paralelo a α
  3. Encontre a distância entre os planos π e α do item anterior
  4. Encontre P em r e Q em l tais que a reta que passa por P e Q seja perpendicular a r e a l .

Passo 1

  1. Temos que mostrar que as retas r e l são reversas. Para isso devemos fazer o produto misto entre os vetores ( A B → ,   r → ,   s → ) e o mesmo deve dar diferente de ZERO.

    2. Vamos primeiro retirar as informações:

    r :   r → = ( 0 ,   1 ,   1 ) R = ( 0 ,   2 ,   1 )               e                   l : l → = ( 1 ,   0 ,   1 ) L = ( 2 ,   3 ,   - 1 )

    Com esses dados vamos montar o produto misto ( R L → ,   r → ,   l → ) :

    R L → = L - R = 2 ,   3 ,   - 1 - 0 ,   2 ,   1 = ( 2 ,   1 ,   - 2 )

    R L → ,   r → ,   l → = 2 1 - 2 0 1 1 1 0 1 2 1 0 1 1 0 = 2 + 1 + 2 = 5

    Portanto, as retas são reversas.

    Passo 2

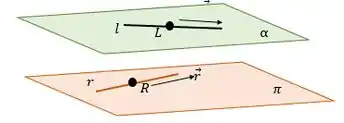
  2. Agora, devemos determinar quais são os planos π e α de forma que: r ⊂ π ,   l ⊂ α e π é paralelo a α . Temos a seguinte figura:

    3. Para determinar um plano temos duas possibilidade: um ponto e seu vetor normal, ouu, dois vetores paralelos ao plano e um ponto. No nosso caso temos a segunda opção, pois temos o vetor diretor da reta que está no plano e além disso o vetor diretor da outra reta é paralelo ao plano, porque o enunciado diz que os planos são paralelos. Assim, com os dois vetores diretores podemos encontrar o vetor normal que será normal à π e a α . Assim, temos:

    r → = 0 ,   1 ,   1         e           l → = ( 1 ,   0 ,   1 )

    Fazendo o produto vetorial entre esses dois vetores obteremos o vetor normal aos planos:

    n → = r → × l → = i → j → k → 0 1 1 1 0 1 i → j → 0 1 1 0 = i → + j → - k →

    n → = ( 1 ,   1 ,   - 1 )

    Tendo o vetor normal ao plano e um ponto pertence à ele, determinamos a equação geral dos planos. Começando com o plano π que possui o ponto R = ( 0 ,   2 ,   1 ) e n → = ( 1 ,   1 ,   - 1 ) ,

    x + y - z + d = 0 → 0 + 2 - 1 + d = 0 → d = - 1

    Portanto, π : x + y - z - 1 = 0

    Fazendo para o plano α que possui o ponto L = ( 2 ,   3 ,   - 1 ) e n → = ( 1 ,   1 ,   - 1 ) :

    x + y - z + d = 0 → 2 + 3 + 1 + d = 0 → d = - 6

    Assim, α : x + y - z - 6 = 0

    Passo 3

  3. Vamos agora calcular a distância entre os plano π e α . Como é a distância entre planos, vamos escolher um ponto de um dos planos e fazer a distância do ponto escolhido até o outro plano. Se escolhermos o ponto R = 0 ,   2 ,   1 = ( x 0 ,   y 0 ,   z 0 ) , então o plano para calcularmos a distância será α : x + y - z - 6 = 0 , teremos a ,   b ,   c , d = ( 1 ,   1 ,   - 1 ,   - 6 ) . Colocando na fórmula, temos:

    4. d P , π = a x 0 + b y 0 + c z 0 + d a 2 + b 2 + c 2 = 1.0 + 1.2 + - 1 . 1 - 6 1 2 + 1 2 + ( - 1 ) 2 = 5 3

    Portanto,a distância entre os planos é d P ,   π = 5 3

    Passo 4

  4. Ufa!! Está quase terminando!! Uhulll

Para finalizar só falta acharmos o ponto P que pertence à r e o ponto Q que pertence à l de forma que a reta que é formada por esses dois pontos seja perpendicular às reta r e l . Então, teremos a seguinte figura:

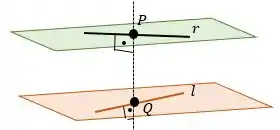
Sabemos que as retas são reversas e vimos na teoria que para achar a distância entre retas reversas precisamos encontrar os ponto P e Q como o enunciado nos pede. Então, vamos primeiro escrever a equação vetorial das retas para então escrevermos os pontos P e Q .

r : X = 0 ,   2 ,   1 + t 0 ,   1 ,   1

l : X = 2 ,   3 , - 1 + h ( 1 ,   0 ,   1 )

Se P pertence à r , então:

P = 0 ,   2 + t ,   1 + t

E Q pertence à l :

Q = ( 2 + h ,   3 ,   - 1 + h )

Se as retas devem ser perpendiculares à reta formada pelo vetor P Q → então, o produto interno entre o vetor P Q → e os vetores diretores deve ser ZERO:

P Q → ∙ r → = 0         e         P Q → ∙ l → = 0        

P Q → = Q - P = 2 + h ,   3 ,   - 1 + h - 0 ,   2 + t ,   1 + t = ( 2 + h ,   1 - t ,   - 2 + h - t )

Fazendo o produto interno:

P Q → ∙ r → = 0 →   2 + h ,   1 - t ,   - 2 + h - t ∙ 0 ,   1 ,   1 = 1 - t - 2 + h - t = 0    

1 - t - 2 + h - t = 0 →

- 2 t + h = 1

P Q → ∙ l → = 0 →   2 + h ,   1 - t ,   - 2 + h - t ∙ 1 ,   0 ,   1 = 2 + h - 2 + h - t = 0

2 h = t

Com esses dois produtos internos temos um sisteminha:

- 2 t + h = 1 2 h = t

Substituindo os valores, temos que:

h = - 1 3

t = - 2 3

Substituindo t e h , achamos P e Q :

P = 0 ,   2 + t ,   1 + t → P = 0 , 4 3 , 1 3

Q = 2 + h ,   3 ,   - 1 + h → Q = 5 3 ,   3 ,   - 4 3

Portanto, chegamos onde queríamos:

P = 0 , 4 3 , 1 3       e       Q = 5 3 ,   3 ,   - 4 3    

Resposta

b) π : x + y - z - 1 = 0       e           α : x + y - z - 6 = 0

c) d P ,   π = 5 3

d) P = 0 , 4 3 , 1 3       e       Q = 5 3 ,   3 ,   - 4 3    

Exercícios de Livros Relacionados

Calcular a distância entre os planos paralelos:a) π 1 : 2 x + 2 y + 2 z - 5 = 0 e π 2 : x + y + z - 3 = 0
Calcular a distância entre os planos paralelos:b) π 1 : x - 2 z + 1 = 0 e π 2 : 3 x - 6 z - 8 = 0
Escrever as equações dos planos paralelos ao plano π : 3 x - 2 y - 6 z - 5 = 0 que distam 5 unidades da origem.
Dê uma equação do plano γ , simétrico de α :x + y - z + 5 = 0 em relação ao plano β :x + y - z - 4 = 0 .
Ache equações paramétricas da reta r ' , simétrica da reta r : x - 1 = y = z em relação ao plano x + y - z - 3= 0 .