Calcule a área do triângulo formado pelos pontos e .
Passo 1
Vamos começar desenhando esse triângulo!
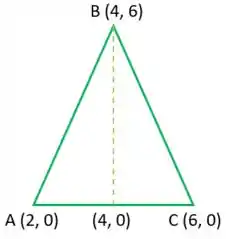
Para calcular a área de um triângulo, faremos:
A altura é a distância do ponto a e a base será a distância de até !
Passo 2
Passo 3
Vamos usar a formulinha para calcular essas distâncias!
Vamos calcular a , sendo e , colocando os valores na fórmula:
Agora :
Show!! Agora é só calcular a área!
Passo 4
A área será:
Sendo e
Resposta
Exercícios de Livros Relacionados
Losango é um paralelogramo cujos lados têm a mesma medida e as diagonais são perpendiculares. A , B , C e D são os vértices consecutivos de um losango. A=( - 1 , - 1,0 ) , B =( 1,4 , a ) e C=( 3,1 , 2
Determine o ponto do segmento A B que está mais próximo de P , e o que está mais afastado.a) A = - 2 ,3 ,3 ,B = 2 ,- 1 ,- 1 ,P = ( - 4 ,1 ,0 )
Descreva o lugar geométrico dos pontos do plano π que equidistam de A e B e comente as peculiaridades geométricas de cada caso.c) π : x - 3 y + z = 0A = 1 ,4 ,0 B = 3 ,- 2 ,2
Calcule a distância entre os pontos P e Q , nos casos:a) P = 0 ,- 1 ,0 ,Q = ( - 1 ,1 ,0 ) b) P = - 1 ,- 3 ,4 ,Q = ( 1 ,2 ,- 8 )
Descreva o lugar geométrico dos pontos do plano π que equidistam de A e B e comente as peculiaridades geométricas de cada caso.b) π : 2 x + 2 y - z = 0A = 0 ,1 , 1 2 B = 2 ,3 ,- 1 2