Sejam os vetores , que vai do ponto até , e , que vai do ponto até . Calcule a maior distância entre eles.
Passo 1
Show! Vamos começar desenhando esses vetores para ver como eles estão posicionados!
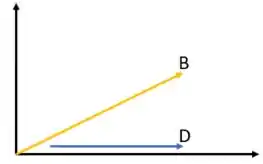
Com esse desenho conseguimos ver que a maior distância entre os vetores acontece na extremidade! Ou seja, entre os pontos e .
Então é só calcular a distância entre esses pontos!
Passo 2
Mais uma vez usaremos a formulinha de distância entre pontos que você já deve estar careca de saber!
Vamos calcular a , sendo e , colocando os valores na fórmula:
Show!! Achamos nossa distância!
Resposta
Exercícios de Livros Relacionados
Losango é um paralelogramo cujos lados têm a mesma medida e as diagonais são perpendiculares. A , B , C e D são os vértices consecutivos de um losango. A=( - 1 , - 1,0 ) , B =( 1,4 , a ) e C=( 3,1 , 2
Determine o ponto do segmento A B que está mais próximo de P , e o que está mais afastado.a) A = - 2 ,3 ,3 ,B = 2 ,- 1 ,- 1 ,P = ( - 4 ,1 ,0 )
Descreva o lugar geométrico dos pontos do plano π que equidistam de A e B e comente as peculiaridades geométricas de cada caso.c) π : x - 3 y + z = 0A = 1 ,4 ,0 B = 3 ,- 2 ,2
Calcule a distância entre os pontos P e Q , nos casos:a) P = 0 ,- 1 ,0 ,Q = ( - 1 ,1 ,0 ) b) P = - 1 ,- 3 ,4 ,Q = ( 1 ,2 ,- 8 )
Descreva o lugar geométrico dos pontos do plano π que equidistam de A e B e comente as peculiaridades geométricas de cada caso.b) π : 2 x + 2 y - z = 0A = 0 ,1 , 1 2 B = 2 ,3 ,- 1 2