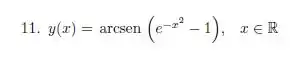Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de EDO com Mudança de Variáveis

Ver Teoria
Exercício 8123456791011121314

Enunciado

Passo 1

A equação do nosso problema é

cos ⁡ ( y ) y ' + 2 x sen ⁡ ( y ) = - 2 x

cos ⁡ ( y ) d y d x + 2 x sen ⁡ ( y ) = - 2 x

E precisamos transformá-la em uma equação linear. Para isso o problema nos sugere que façamos a substituição

z = sen ⁡ y

Para isso precisamos encontrar d z

d z d y = cos ⁡ ( y )

Passo 2

Fazendo a substituição ficaremos com

cos ⁡ ( y ) d y d x + 2 x sen ⁡ ( y ) = - 2 x

d z d y d y d x + 2 x z = - 2 x

Agora nossa expressão é

d z d x = - 2 x - 2 x z

d z d x = - 2 x ( 1 + z )

Percebeu que temos uma equação linear agora? Tem outra coisa, ela também é separável.

Passo 3

Para resolver uma equação separável basta passar tudo que for variável z para um lado e tudo que for x para o outro e integrar os dois lados.

d z d x = - 2 x ( 1 + z )

d z ( 1 + z ) = - 2 x   d x

∫ d z ( 1 + z ) = ∫ - 2 x   d x

Passo 4

Para integrar

∫ d z ( 1 + z )

Vamos usar a substituição

u = 1 + z

d u = d z

Então

∫ d z ( 1 + z ) = ∫ d u u = ln ⁡ u

= ln ⁡ 1 + z

E a integral

∫ - 2 x   d x = - 2 ∫ x   d x

= - x 2 + C '

Repare que teríamos uma constante de integração para cada integral, mas para simplificar as coisas podemos uni-las em apenas uma constante C ' .

Passo 5

Juntando os dois lados da equação

∫ d z ( 1 + z ) = ∫ - 2 x   d x

ln ⁡ 1 + z = - x 2 + C '

1 + z = e - x 2 e C '

z = e - x 2 e C ' - 1

Podemos agora desfazer a substituição do passo 1.

z = sen ⁡ y

sen ⁡ y = e - x 2 e C ' - 1

y ( x ) = arcsen ⁡ e - x 2 e C ' - 1

Como dado no enunciado , y 0 = 0 . Então

y 0 = arcsen ⁡ e - 0 2 e C ' - 1 = 0

Então C ' = 0 e

y ( x ) = arcsen ⁡ e - x 2 - 1

Resposta

Exercícios de Livros Relacionados

Nos problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada.1. x e 2 y . d y d x + e 2 y = ln ⁡ x x
Nos Problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada. 2 y y ' + x 2 + y 2 + x = 0
Nos Problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada. y ' = y + x y + 1 2 + 1
Nos Problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada. sen ⁡ ys e n hxd x + cos ⁡ y cosh ⁡ xd y = 0
Nos Problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada. d y d x - 4 x y = 2 x 5 e y x 4