Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de EDO com Mudança de Variáveis

Ver Teoria
Exercício 1312345678910111214

Enunciado

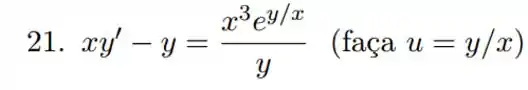
Passo 1

Fazendo a substituição:

y = x u

Logo

d y d x = u ' x + u

Substituindo isso na equação vamos ter

x u ' x + u - x u = x 3 e u x u

Arrumando essa equação

x 2 u ' = x 2 y u u

Então:

u ' = e u u

d u d x u e - u = 1

Essa equação vai ser separável.

Passo 2

Vamos resolver essa equação separável

u e - u d u = d x

Integrando dos dois lados

∫ u e - u d u = ∫ d x

e - u u + 1 = x + C

Passo 3

A solução dessa equação envolve na verdade x e y , então temos que voltar para y , lembrando que

y = u x

Temos

u = y x

E a nossa solução vai ser

e - y x y x + 1 = x + C

Arrumando:

y + x = x x + C e y x

Resposta

y + x = x x + C e y x

Exercícios de Livros Relacionados

Nos problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada.1. x e 2 y . d y d x + e 2 y = ln ⁡ x x
Nos Problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada. 2 y y ' + x 2 + y 2 + x = 0
Nos Problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada. y ' = y + x y + 1 2 + 1
Nos Problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada. sen ⁡ ys e n hxd x + cos ⁡ y cosh ⁡ xd y = 0
Nos Problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada. d y d x - 4 x y = 2 x 5 e y x 4