Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de EDO com Mudança de Variáveis

Ver Teoria
Exercício 9123456781011121314

Enunciado

Nos exercícios 19 a 21 use o método desenvolvido na questão 18, para determinar a solução geral das equações.

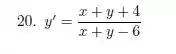
Passo 1

Nessa questão nós vamos fazer uma substituição baseada na teoria que apareceu no exercício 18. A primeira coisa que devemos fazer é identificar qual substituição iremos usar. Lembrando o formato da equação do exercício 18.

d y d x = F a x + b y + c A x + B y + C

Na nossa EDO teremos.

a = b = A = B = 1 ,     c = 4 ,     C = - 6

Como a b = A B = 1 , vamos usar a seguinte substituição.

z = x + y

d z d x = 1 + d y d x

Passo 2

Realizando a mudança de variável teremos.

d z d x - 1 = z + 4 z - 6

d z d x = 2 z - 2 z - 6

z - 6 2 z - 2 d z = d x

Agora basta resolvermos essa equação separável.

Passo 3

Integrando dos dois lados da equação teremos

∫ z - 6 2 z - 2 d z = 1 2 ∫ z - 1 - 5 z - 1 d z = 1 2 ∫ d z - 5 ∫ 1 z - 1 d z

∫ z - 6 2 z - 2 d z = 1 2 z - 5 ln ⁡ z - 1

∫ d x = x

Passo 4

Igualando as duas equações e somando uma constante de Integração D

1 2 z - 5 ln ⁡ z - 1 = x + D

z - 5 ln ⁡ z - 1 = 2 x + 2 D

Substituindo z = x + y e 2 D = C

y - x - 5 ln ⁡ x + y - 1 = C

Resposta

Exercícios de Livros Relacionados

Nos problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada.1. x e 2 y . d y d x + e 2 y = ln ⁡ x x
Nos Problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada. 2 y y ' + x 2 + y 2 + x = 0
Nos Problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada. y ' = y + x y + 1 2 + 1
Nos Problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada. sen ⁡ ys e n hxd x + cos ⁡ y cosh ⁡ xd y = 0
Nos Problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada. d y d x - 4 x y = 2 x 5 e y x 4