Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de EDO com Mudança de Variáveis

Ver Teoria
Exercício 1012345678911121314

Enunciado

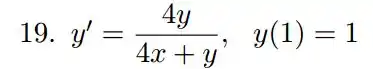
Passo 1

Repara que essa nossa equação tem funções polinomiais, então é interessante olharmos se essa função é homogênea.

Assim temos

f x , y = 4 y 4 x + y

Agora fazemos f λ x , λ y para ver se é igual a f x , y ,

f λ x , λ y = 4 λ y 4 λ x + λ y = 4 y 4 x + y

Logo vamos ter

f λ x , λ y = f x , y

E essa equação vai ser homogênea

Passo 2

Para resolver uma equação homogênea nos fazer

y = z x

Logo

d y d x = d z d x x + z

Substituindo isso na equação vamos ter

d z d x x + z = 4 z x 4 x + z x

Arrumando essa equação

d z d x x + z = 4 z 4 + z

d z d x x = 4 z 4 + z - z

d z d x x = - z 2 4 + z

Essa equação vai ser separável.

Passo 3

Vamos resolver essa equação separável

d z d x x = - z 2 4 + z

Multiplicando cruzado para ter tudo com z de um lado e tudo com x do outro, vamos ter

- 4 + z z 2 d z = d x x

4 z 2 + 1 z d z = - d x x

Integrando dos dois lados

∫ 4 z 2 + 1 z d z = - ∫ d x x

- 4 z + ln ⁡ z = - ln ⁡ x + C

Passo 4

A solução dessa equação envolve na verdade x e y , então temos que voltar para y , lembrando que

y = z x

Temos

z = y x

E a nossa solução vai ser

- 4 x y + ln ⁡ y x = - ln ⁡ x + C

Arrumando:

- 4 x y + ln ⁡ y = + C

Então:

y = C e 4 x y

Passo 5

Agora temos que achar essa constante C fazendo o valor inicial que ele deu

y 1 = 1

Então

1 = C e 4 1

Então

C = e - 4

E nossa solução vai ser

y = e - 4 e 4 x y = e 4 x - y y

Resposta

y =   e 4 x - y y

Exercícios de Livros Relacionados

Nos problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada.1. x e 2 y . d y d x + e 2 y = ln ⁡ x x
Nos Problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada. 2 y y ' + x 2 + y 2 + x = 0
Nos Problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada. y ' = y + x y + 1 2 + 1
Nos Problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada. sen ⁡ ys e n hxd x + cos ⁡ y cosh ⁡ xd y = 0
Nos Problemas 1-26, resolva a equação diferencial dada usando uma substituição apropriada. d y d x - 4 x y = 2 x 5 e y x 4