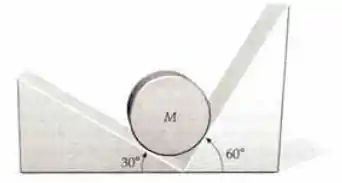
Um cilindro de massa está apoiado sobre uma calha sem atrito, formada por um plano inclinado de com a horizontal, à esquerda, e outro plano inclinado de , à direita, como mostrado na figura abaixo. Determine a força exercida por cada plano sobre o cilindro.
Passo 1
Vamos começar montando a figura. Temos um cilindro entre dois planos inclinados sem atrito.
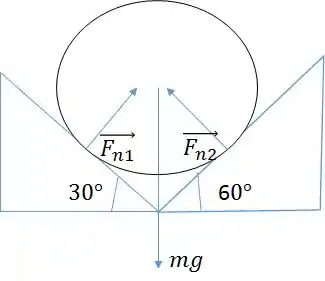
É possível perceber que tem duas forças normais e a força peso do cilindro, conforme mostra a figura abaixo:
Passo 2
Como a situação é de equilíbrio, vamos usar as condições de equilíbrio:
Mas antes disso, temos que decompor e .
A ideia é descobrir a inclinação dessas forças. Montamos, então, a seguinte figura:
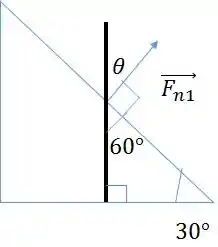
Perceba que descobrindo o valor de , podemos decompor em e .
Montando esse triângulo, fica fácil de ver que .
De forma análoga, no plano de , temos a seguinte figura:
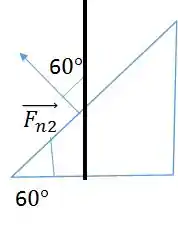
Show! Agora já podemos decompor as forças (lembre-se cosseno lado colado ao ângulo e seno lado oposto) e utilizar as equações.
Passo 3
Começando por:
Agora podemos utilizar a outra equação:
Substituindo o valor de :
Podemos agora descobrir o valor de :