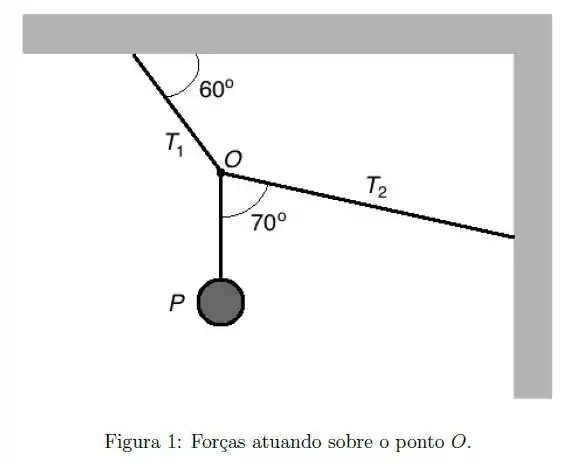
O ponto indicado por O na figura está em equilíbrio sob a ação de três forças: o peso do corpo e as tensões e
- Desenhe o diagrama de corpo livre mostrando as forças que atuam sobre O
- Se , quais os vetores dos módulos de e ?
Passo 1
Oi, tudo bem? Vou te ajudar nessa questão, bora começar?
Letra (a) Temos um sistema em equilíbrio, não é mesmo? E o que isso significa?
Significa que a força resultante é igual a zero!

E o que isso influencia no cálculo das tensões? Se você olhar com carinho a figura do enunciado, verá que as tensões fazem um ângulo com os eixos e (imaginários por enquanto), e assim teremos componentes verticais e horizontais dessas forças
Quando o sistema está em equilíbrio, a soma de todas as componentes é zero, assim como todas as componentes em . E é usando esse fato que vamos determinar as tensões!

Mas pode ficar tranquilo, vou fazer passo a passo com você!
Passo 2
Letra (a): vamos olhar com mais carinho para o desenho do nosso sistema:
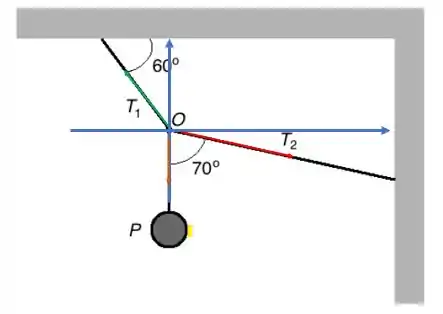

O nosso diagrama de corpo livre é esse aí! Desenhamos em cima do ponto O todas as forças que agem!
Bora calcular essas componentes?
Passo 3
Letra (b): agora o problema diz que , e pede para calcularmos os valores de e . Bom, para isso vamos retornar ao nosso diagrama de forças do passo anterior, mas agora olhando as componentes dos vetores!
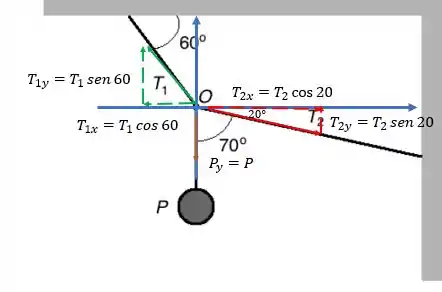
Com as componentes podemos agora fazer a soma em cada direção (x e y) e igualar a zero:
- Em :
- Em :
Tudo bem até aqui?
Sendo assim ficamos com esse sistema de equações:

nossa missão agora é resolver esse sistema para encontrar o módulo das tensões e
Passo 4
Temos esse sistema aqui
Vamos isolar da segunda equação e substituir na primeira. Bora lá?

E colocando na primeira
Organizando um pouco temos
Agora multiplicando tudo por e isolando :
Oba! Primeira componente encontrada com sucesso! #partiu achar a segunda? Lembra que isolamos lá no começo desse passo?
Agora que temos o valor de é só substituir
Perfeito! Espero ter ajudado! Vamos praticar mais?