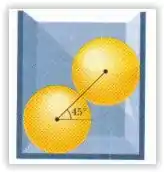
Na figura abaixo, duas esferas idênticas uniformes e sem atrito, de massa m, respousam em um recipiente retangular rígido. Uma reta que liga os centros das esferas está a com a horizontal. Determine o módulo das forças exercidas sobre as esferas:
- pelo fundo do recipiente
- pela parede lateral esquerda do recipiente
- pela parede lateral direita do recipiente
- por uma das esferas sobre a outra.
(Sugestão: A força de uma esfera sobre a outra aponta ao longo da reta que passa pelo centro)
Passo 1
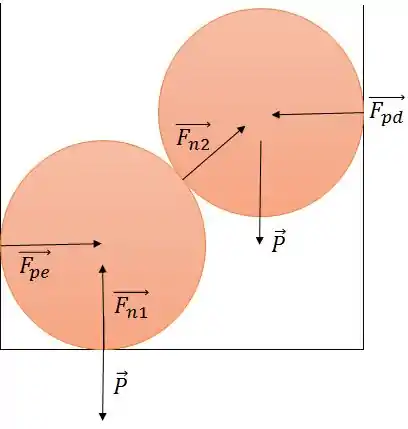
Vamos primeiro marcar as forças.
Temos:
: A força que a parede direita exerce sobre a esfera
: A força que a parede esquerda exerce sobre a esfera
: O peso da bola
: A força normal do chão na bola debaixo
: A força de contato entre as duas esferas
Passo 2
Agora, vamos decompor em e para podermos aplicar as condições de equilíbrio.
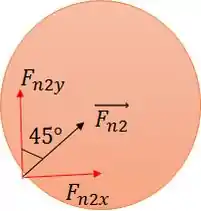
Podemos ver pela figura acima que
Passo 3
Agora, podemos aplicar as condições de equilíbrio para descobrirmos a força , ou seja, a força normal do chão na bola debaixo. Para isso, vamos analisar as duas esferas como um único bloco.
Quando analisamos as duas esferas juntas, pela terceira lei de newton (ação e reação), a vai se anular com uma força de mesmo módulo e sentido oposto exercida sobre a esfera debaixo pela esfera de cima.
Assim, vamos utilizar a condição de equilíbrio: .
Como só temos as duas forças peso para baixo e para cima.
Passo 4
Vamos calcular primeiro a força que a parede exerce na bola direita. Para isso vamos analisa-la separadamente.
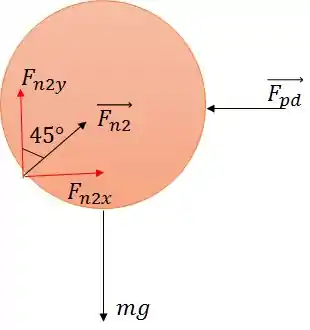
Vemos por que
Logo, podemos descobrir
Aplicando
Passo 5
Para analisar a força da parede esquerda, podemos analisar as duas esferas juntas. Lembrando que quando analisamos as duas juntas a forças de ação e reação de uma esfera sobre a outra se anulam.
Assim, aplicando
Passo 6
A força de uma esfera sobre a outra já foi achada no passo 4
Como
Então,