Os diagramas abaixo mostram forças aplicadas a uma roda de peso igual a . A roda é livre para girar e transladar. O módulo de é igual a . Em qual(is) diagrama(s) a roda estará em equilíbrio?
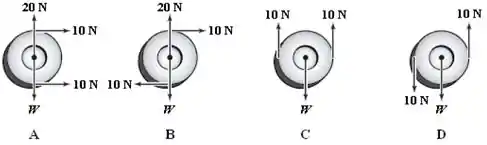
(A)
(B)
(C)
(D)
(E) e
Passo 1
Para que a roda esteja em equilíbrio, ela deve atender a duas condições:
Soma das forças e soma dos torques igual a zero.
Vamos ver cada um dos casos.
Passo 2
Diagrama :
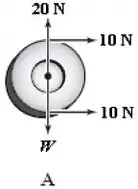
Como é igual a , temos equilíbrio na vertical:
Já na horizontal, não temos equilíbrio:
Então, já descartamos esse diagrama, por mais que o torque resultando seja nulo.
Passo 3
Diagrama :
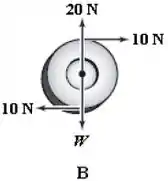
Nesse caso a força resultante é nula tanto na vertical quanto na horizontal:
Vamos ao torque resultante...
As forças que estão aplicadas no centro da roda não geram torque com relação a esse ponto.
Já as forças de aplicadas na borda geram um torque, sendo os dois no sentido horário:
Então, a roda desse diagrama também não est[a em equilíbrio.
Passo 4
Diagrama :
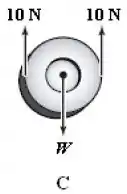
Nesse diagrama temos um equilíbrio de forças:
Vamos ao torque...
Se calcularmos o torque com relação ao centro da roda, a força não gera torque pois está aplicada nesse ponto.
Já o torque das outras duas forças se cancelam, pois um é para o sentido horário e o outro é para o sentido anti-horário:
Esse diagrama está em equilíbrio!
Passo 5
Diagrama :
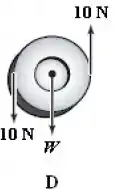
Logo de cara, já não temos um equilíbrio de forças:
Então, já descartamos esse diagrama também.
Passo 6
Ao todo, apenas o diagrama está em equilíbrio, ou seja, tanto de forças quanto de torques.
Ficamos com a letra (C).
Resposta
Letra (C)