O sistema mostrado na figura está em equilíbrio estático. A haste, de comprimento e massa , é mantida na posição vertical. O topo da haste é preso a uma parede vertical por um fio e uma força é aplicada ao ponto médio da haste. O coeficiente de atrito estático entre a haste e a superfície horizontal é . Qual é a máxima força que pode ser aplicada para que a barra ainda permaneça em equilíbrio estático?
a) ;
b) ;
c) ;
d) ;
e) ;
Passo 1
A haste está presa por um fio que exerce uma força de tração na parte de cima. Além disso, aparece também uma força de atrito no chão, impedindo ela de deslizar.
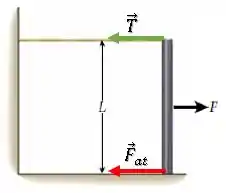
À medida que a força vai aumentando, a também aumenta mantendo a barra em equilíbrio.
A situação limite é quando a atinge o valor de força de atrito estático máxima, pois a partir daí, a escada irá deslizar.
Então, para achar máximo, consideraremos a também máxima, calculada pela expressão:
Passo 2
Fazendo o equilíbrio de forças na horizontal, achamos que:
Entretanto, não sabemos nada sobre a força de tração . Então devemos aplicar a equação de momento no ponto preso pela corda (ponto A), pois ela sairá da equação (torque nulo).
Como a haste está em equilíbrio, o somatório de momentos em qualquer ponto é nulo:
Vamos olhar para todas as forças na haste:
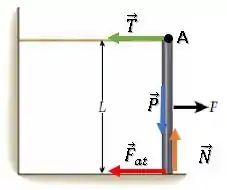
O somatório dos torques em A é:
A força está aplicada no ponto A, portanto seu torque é nulo.
As forças e têm sua direção passando pelo ponto A, portanto seus torques também serão nulos.
O valor do torque da força é:
Pelo equilíbrio na vertical:
Então:
Já o valor do torque da força é:
Voltando ao somatório de torques, temos que a força tenta girar a haste em torno de A no sentido horário enquanto a força tenta girá-la no sentido anti-horário. Logo, seus torques têm sinais contrários.
Então, achamos que a força máxima é:
Ficamos com a letra (a).
Resposta
Letra (a)