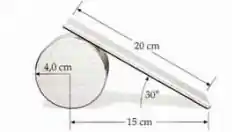
A figura abaixo mostra uma prancha homogênea de de comprimento, sobre um cilindro de de raio. A massa da prancha é e a do cilindro . O coeficiente de atrito estático entre a prancha e o cilindro é zero, enquanto os coeficientes de atrito estático entre o cilindro e o piso, e entre a prancha e o piso, não são nulos. Existem valores, para estes coeficientes de atrito estático, para os quais o sistema fique em equilíbrio estático? Caso afirmativo, que valores são esses? Caso negativo, explique o porquê de sua não existência.
Passo 1
Vamos primeiro montar o diagrama das forças do problema.
Se liga!
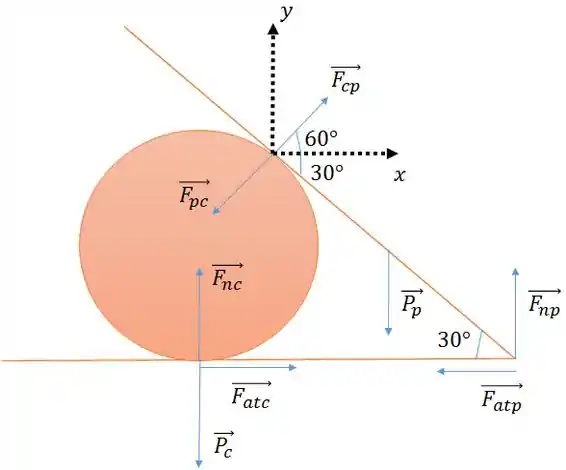
Calma! Ficou confuso, né? Vou explicar cada coisa.
é a força normal que o chão exerce na prancha
é a força normal que o chão exerce no cilindro
é a força de atrito na prancha
é a força de atrito no cilindro
é o peso da prancha, localizado em seu centro de massa
é o peso do cilindro, localizado em seu centro de massa
é a força que a prancha exerce no cilindro
é a força que o cilindro exerce na prancha
Por serem forças de ação e reação, elas são iguais:
Muitas forças, né? Isso é chatinho. Mas isso acontece porque são dois corpos encostados no chão. Então temos peso, normal e atrito para cada um.
Não podemos esquecer do ângulo fornecido. Podemos descobrir a inclinação de .
Primeiro utilizamos uma transversal cortando duas retas paralelas: ângulos alternos internos são iguais!
Depois, utilizamos o fato de que a força é perpendicular a superfície. Logo, o ângulo é de .
Muita coisa, né? Mas já é um adianto enorme no problema.
Passo 2
Como o enunciado pede uma relação dos coeficientes de atrito, vamos escrevê-los na forma das forças acima. Lembre-se que .
Vamos achar:
: O coeficiente de atrito do cilindro com o chão
: O coeficiente de atrito da prancha com o chão
Utilizando a fórmula que relaciona coeficiente de atrito com força normal e força de atrito, chegamos ao seguinte resultado:
Percebeu que se a gente descobrir o valor dessas forças, a gente descobre os coeficientes de atrito que garantem o equilíbrio?
Passo 3
Vamos aplicar agora as condições de equilíbrio.
Vamos começar pela condição de na prancha.
Para isso, escolheremos o eixo de rotação no ponto em que a prancha encontra o chão. Assim, a força de atrito e a força normal não geram torque. As duas forças que geram torque na prancha são e .
A distância de até o eixo é de .
A distância perpendicular de até o eixo de rotação é de Repare na figura abaixo:
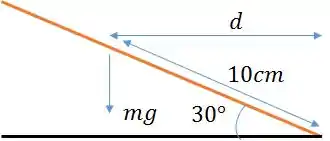
Assim, podemos montar a equação do torque, escolhendo o sentido anti-horário como positivo.
Passo 4
Vamos continuar analisando a prancha.
Podemos aplicar agora as outras condições de equilíbrio:
Antes disso, vamos decompor em e
Dá uma olhada na figura abaixo:
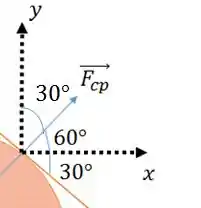
Passo 5
Vamos aplicar para descobrirmos o valor de
Passo 6
Já temos a força normal no ponto em que a prancha encontra o chão. Precisamos da força de atrito no mesmo ponto.
Vamos aplicar para descobrirmos o valor de .
Passo 7
Agora que temos e , podemos calcular o coeficiente de atrito entre a prancha e o chão.
Passo 8
Falta descobrirmos o coeficiente de atrito estático entre o cilindro e o chão.
Então, temos que encontrar e .
Para isso vamos utilizar as equações de equilíbrio para o cilindro.
Já sabemos que por serem forças de ação e reação, as forças e são iguais.
A força tem o mesmo módulo da força e sentido contrário.
A força tem o mesmo módulo da força e sentido contrário.
Passo 9
Vamos aplicar para o cilindro para descobrirmos o valor de .
Passo 10
Já temos a força normal no ponto em que o cilindro encontra o chão. Precisamos da força de atrito no mesmo ponto.
Vamos aplicar para descobrirmos o valor de .
Passo 11
Agora que já temos e podemos achar o coeficiente de atrito entre o cilindro e o chão.
Fim!!! Achamos os valores dos coeficientes de atrito que garantem o equilíbrio estático!
Resposta
Coeficiente de atrito estático entre a prancha e o chão:
Coeficiente de atrito estático entre o cilindro e o chão: