Uma escada homogênea com de peso está apoiada em uma parede vertical sem atrito. A base da escada está apoiada no solo e uma estaca presa ao solo a impede de escorregar. A escada faz um ângulo de com a horizontal. A força que a escada exerce sobre a parede é de aproximadamente:
(a) ;
(b) ;
(c) ;
(d) ;
(e) ;
Passo 1
Quais são as forças atuando sobre a escada?
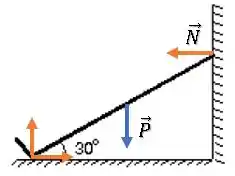
Temos as reações do apoio na estaca, a força peso e a força normal da parede, que deve estar perpendicular à superfície.
Se temos o valor da força peso e queremos a força normal, podemos usar a equação de equilíbrio dos torques no apoio da estaca:
Os torques das forças aplicadas no próprio apoio são nulos, logo resta o torque da força peso e o torque da normal:
Passo 2
Sobre a força peso, se a escada é homogênea (massa uniformemente distribuída), podemos considerar que seu centro de gravidade (ponto de aplicação de ) está no meio da escada.
Vamos chamar o comprimento da escada de , então, sua distância perpendicular à força será a projeção na horizontal de metade da escada:
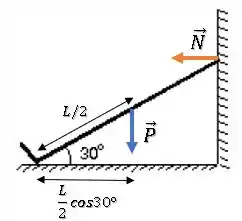
Logo, o torque da força peso é o produto da distância com a força:
Enquanto a distância perpendicular à força normal é:
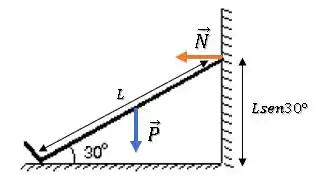
Logo, o torque da força normal é o produto da distância com a força:
Voltando à nossa equação de equilíbrio:
Só que a força peso tenta girar a escada no sentido horário enquanto a força normal tenta girar a escada no sentido anti-horário, portanto seus torques terão sinais opostos:
Podemos cortar o tamnho da escada :
Logo, a força que a parede exerce sobre a escada é aproximadamente:
Ficamos com a alternativa (a).
Resposta
Letra (a)