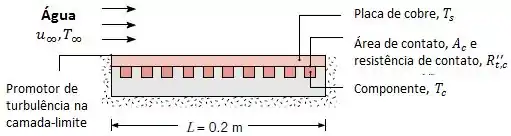
Cem componentes elétricos, cada um dissipando , estão fixados a superfície de uma placa quadrada de cobre , e toda a energia dissipada é transferida para a água que se encontra em escoamento paralelo sobre a superfície oposta.
Uma protuberância na aresta frontal da placa atua na perturbação da camada-limite e a placa pode ser considerada isotérmica. A velocidade e a temperatura d água são e , e as propriedades termofísicas da água podem ser aproximadas por , e .
Qual é a temperatura da placa de cobre?
Se cada componente possui uma área superficial de contato com a placa de cobre igual a e a resistência térmica de contato é igual a , qual é a temperatura dos componentes? Despreze a variação de temperatura ao longo da espessura da placa de cobre.
Passo 1
Qual é a temperatura da placa de cobre?
Da equação da taxa de transferência de calor por convecção, temos que:
Podemos reorganizar essa equação e encontrar a temperatura na superfície da placa:
Show de bola! Precisamos calcular o coeficiente convectivo médio pra resolver o problema.
Passo 2
Nesse caso, o problema foi até bom com a gente, porque ele já nos deu as propriedades da água e nos disse que o escoamento ao longo de toda a placa é turbulento. Ou seja, podemos utilizar a seguinte expressão para o número de Nusselt médio:
Substituindo os valores:
Passo 3
O coeficiente convectivo médio será dado por:
Passo 4
Substituindo o valor de na expressão que chegamos no Passo 1, teremos:
Obs.: Multiplicamos a taxa de transferência de calor por 100 pois estamos trabalhando com cem componentes elétricos.
Passo 5
Se cada componente possui uma área superficial de contato com a placa de cobre igual a e a resistência térmica de contato é igual a , qual é a temperatura dos componentes? Despreze a variação de temperatura ao longo da espessura da placa de cobre.
Levando em conta a resistência de contato, a taxa de transferência de calor através de cada componente será dada por:
Reorganizando a equação, teremos:
Substituindo os valores:
Obs.: .
![]()
Resposta
![]()