Uma placa plana, com largura de , é mantida a uma temperatura superficial uniforme pelo uso de módulos retangulares geradores de calor, com espessura e comprimento , que são controlados independentemente. Cada módulo encontra-se isolado de seus vizinhos, bem como em sua superfície inferior.
Ar atmosférico a escoa sobrea a superfície da placa a uma velocidade de . As propriedades termofísicas dos módulos são , e .
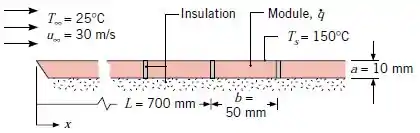
Determine a geração de energia necessária, , em um módulo posicionado a uma distância de da aresta frontal.
Determine a temperatura máxima neste módulo de geração.
Passo 1
Determine a geração de energia necessária, , em um módulo posicionado a uma distância de da aresta frontal.
Vamos nessa! Queremos encontrar a geração de energia , , para isso considerando o balanço de energia, temos:
Sabendo que:
e
Substituindo, as expressões a cima, podemos calcular :
Passo 2
Agora, que sabemos como calcular precisamos achar o coeficiente médio de convecção ():
O problema nos deu as propriedades do módulo, mas não nos deu as propriedades do ar. Assim, usando a temperatura de filme como referência, temos que:
Sabendo a temperatura de filme, podemos achar as propriedades do ar.
De acordo com a tabela A.4 do Incropera, temos que:
Passo 3
Com as propriedades dos fluidos em mãos, podemos calcular o número de Reynolds:
Como estamos interessados no módulo a da aresta frontal, . Dessa forma:
Opa! . O escoamento não é laminar nessa região!
Passo 4
A questão agora é a seguinte! Como estamos interessados em calcular a taxa de transferência de calor do módulo localizado a da aresta frontal da placa, não é uma boa usarmos a expressão para o número de Nusselt médio, porque ele vai nos dar o coeficiente convectivo médio ao longo de todos os .
Nesse caso, o coeficiente convectivo médio desse módulo que estamos interessados vai ser aproximadamente igual ao coeficiente convectivo local no centro desse módulo.
Então, vamos utilizar o número de Nusselt local no centro do módulo.
Já calculamos o número de Reynold para , mas agora estamos interessados em uma nova posição, no centro do módulo que tem comprimento .
Dessa forma, vamos calcular o novo número de Reynolds, agora para :
Como sabemos que o escoamento é turbulento em toda placa, vamos usar a seguinte correlação:
Substituindo os valores:
Passo 5
O coeficiente convectivo médio no módulo será, então:
Substituindo os valores:
Passo 6
Agora que achamos finalmente temos todas as variáveis necessárias pra calcular a geração de energia necessária (, que será:
Passo 7
Determine a temperatura máxima neste módulo de geração.
O fluxo de energia gerada no módulo deve ser igual ao fluxo de calor por condução no mesmo.
Partindo do princípio que a energia é gerada no centro do módulo, a temperatura será máxima neste mesmo ponto, a uma distância da superfície do módulo. Logo:
Reorganizando a equação:
Substituindo os valores:
Resposta