Placas de aço (AISI 1010), de espessura e lados de comprimento , são transportadas na saída de um processo de tratamento térmico e simultaneamente resfriadas por ar atmosférico com velocidade e em escoamento paralelo sobre as placas.
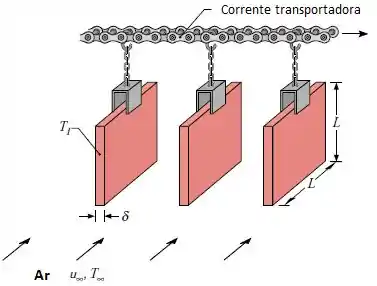
Para uma temperatura da placa inicial de , qual é a taxa de transferência de calor saindo da placa? Qual é a taxa de variação da temperatura da placa correspondente? A velocidade do ar é muito maior do que a velocidade da placa.
Passo 1
Antes de qualquer coisa, precisamos definir as propriedades dos materiais.
Para o aço (AISI 1010), vamos usar como referência a temperatura inicial da placa . Dessa forma, de acordo com a tabela A.1 do Incropera:
Já para o ar, vamos usar como referência a temperatura de filme . De acordo com a tabela A.4 do Incropera:
Passo 2
Para calcular a taxa de transferência de calor, vamos precisar do coeficiente convectivo médio mas, antes disso, precisamos calcular o número de Reynolds pra decidir qual correlação vamos usar:
Logo, vamos usar a correlação de para escoamento laminar.
Passo 3
A correlação adequada é a seguinte:
Substituindo os valores:
Passo 4
O coeficiente convectivo médio será dado por:
Passo 5
Finalmente, a taxa de transferência de calor será dada por:
Como o ar escoa pelos dois lados da placa, , onde corresponde à área de cada lado da placa. Logo:
![]()
Passo 6
Fazendo o balanço de energia na placa, temos que:
Como não temos energia entrando e sendo gerada na placa:
Dessa forma:
Reorganizando os tempos da equação, a taxa de variação da temperatura da placa correspondente será:
Substituindo os valores:
Resposta
![]()
![]()