Uma placa plana quadrada de de lado tem uma de suas faces imersa em um meio com ar a que escoa paralelamente a placa com uma velocidade de . A outra face está exposta a uma chama. Essa chama está a e um coeficiente de película de pode representar a transferência de calor homogênea na área dessa face.
A placa é feita de aço inoxidável 304, as propriedades do aço podem ser consideradas constantes e iguais a seus valores a e essa placa possui uma espessura de .
Considerando que o sistema está em estado estacionário e que a radiação térmica pode ser desprezada. E sabendo que as propriedades termofísicas do ar podem ser obtidas pela tabela anexa do livro de referência e que esse se comporta como gás ideal.
Determine a temperatura na superfície de cada face da placa e a taxa de transferência de calor associada ao sistema.
Passo 1
A estratégia aqui é a seguinte: ao invés de começar calculando as temperaturas pra depois calcular a taxa de transferência de calor, vamos fazer o contrário.
Para isso, vamos analisar o problema como o seguinte circuito térmico:
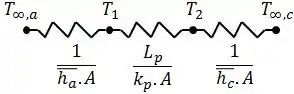
Onde os índices , e correspondem ao ar, à placa e à chama, respectivamente, e e representam as temperaturas das faces da placa.
Nesse caso, a taxa de transferência de calor será:
Onde a resistência térmica equivalente é dada por:
De acordo com a tabela A.1 do Incropera, para o aço inoxidável 304 a , a condutividade térmica será:
Repare que, da equação resistência térmica equivalente, o único valor que não conhecemos é o coeficiente convectivo entre a placa e o ar. Então vamos atrás dele.
Passo 2
Esse se trata de um problema de convecção externa. Assim, as propriedades do ar deveriam ser dadas à temperatura de filme, dada por:
Mas como não temos , vamos utilizar aqui a temperatura de , que o problema nos deu para calcular as propriedades do aço.
Assim:
Assim, utilizaremos os dados tabelados para . De acordo com a tabela A.4 do Incropera, para o ar a esta temperatura:
Passo 3
O número de Reynolds, será:
Opa! Como estamos interessados em calcular o coeficiente convectivo médio, vamos usar a correlação do número de Nusselt para a região de transição (considerando ), dada por:
Substituindo os valores:
Assim, o coeficiente convectivo entre a placa e o ar será:
Passo 4
A resistência térmica equivalente do circuito será:
Passo 5
A taxa de transferência de calor será:
Passo 6
A temperatura na parede em contato com o ar será:
Substituindo os valores:
Passo 7
A temperatura na parede em contato com a chama será:
Substituindo os valores: