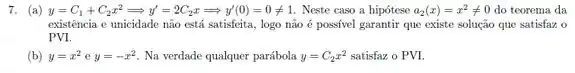Passo 1
a)
A primeira coisa que ele pede é pra mostrarmos que não tem como existir uma solução para aquelas condições iniciais. Para descobrirmos isso devemos substituir os valores.
Isso é impossível, logo não existem constantes para formar uma solução com essas condições iniciais.
Passo 2
A segunda parte desse item é pra explicar porque isso não é uma violação do Teorema da Existência e Unicidade. Vamos escrever a forma completa da nossa EDO e analisar o teorema nela.
Temos que essas funções logo acima devem ser continuar num intervalo contendo, nesse caso, 0 e que . Que todas essas funções são continuas em todos os reais tá bem na cara, vamos analisar a outra condição então.
Tá ai o porquê disso não violar o teorema. O teorema não vai garantir existência de solução porque a condição inicial do problema é para e o teorema diz que não podemos pegar justamente esse ponto.
Passo 3
b)
O teorema não garante a existência de solução para mas também não impede de existir. Vamos substituir os valores dados e encontrar duas soluções dadas pra condição inicial dada nesse item.
Logo, qualquer solução com vai ser solução., como por exemplo
Resposta