Um laser de intensidade produz um feixe de radiação cilíndrico e com seção reta de raio . O feixe incide perpendicularmente sobre uma placa esférica totalmente negra, de raio , com .
Modelando a frente de onda como plana e monocromática, qual é a força exercida pela radiação sobre a placa?
Passo 1
O enunciado quer a força exercida pela radiação sobre a placa. Um problema assim, a estrutura é sempre: achar a pressão da radiação e multiplicar pela área que ela ilumina.
Nesse caso, a placa esférica é totalmente negra, o que implica que ela é uma absorvedora perfeita: Toda a radiação vai ser absorvida.
Logo, a pressão vai ser:
Passo 2
Agora precisamos da área que ela vai iluminar.
Um certo cuidado aqui é necessário. Quando ele fala sobre uma “placa esférica”, isso não significa que ela é literalmente uma esfera. Se fosse assim, a área iluminada seria a de uma calota da esfera, visto que o raio do cilindro é menor que o raio da placa.
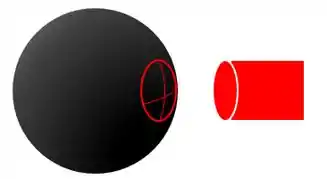
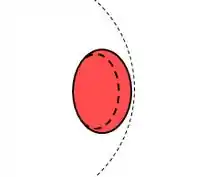
Porém, a idéia aqui é que é uma “placa”. Não faz sentido uma placa ser uma esfera. Então o que ele quer dizer é uma placa redonda maior que o feixe de luz.
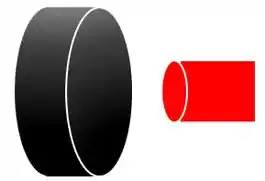
Assim, a área da região iluminada é igual a área da seção circular do feixe de luz, que vai ser:
(obs: uma segunda forma de imaginar essa discussão é imaginando uma esfera tão maior que o feixe, que ela seria aproximadamente plana onde a luz incide, dando a mesma área).
Logo, a força realizada pela radiação será:
A resposta então é a letra (a).
Resposta
Letra a)