Vetor de Poynting e Pressão de Radiação
Um laser de intensidade produz um feixe de radiação monocromático, cilíndrico e com seção reta de raio . O feixe incide perpendicularmente sobre uma placa que o absorve totalmente.
Calcule a potência média emitida pelo laser.
Calcule a amplitude do campo elétrico e do campo magnético do feixe incidente.
Calcule a força exercida pela radiação sobre a placa.
Calcule a densidade volumétrica média de energia do feixe.
Passo 1
Calcule a potência média emitida pelo laser.
A intensidade do laser, por definição, é dada por:
E a potência do vetor de Poynting é dada por:
Assim, a potência média será dada por:
Onde corresponde à área da seção transversal do laser:
Passo 2
Calcule a amplitude do campo elétrico e do campo magnético do feixe incidente.
Trabalhando, novamente, com a definição de intensidade do laser, teremos:
Para calcular cada um deles, vamos usar a relação . Sendo assim:
Novamente, usando a expressão , teremos:
Passo 3
Calcule a força exercida pela radiação sobre a placa.
Quando a onda é completamente absorvida, calculamos a pressão de radiação por
A pressão está relacionada com a força por:
Logo:
Passo 4
Calcule a densidade volumétrica média de energia do feixe.
Conforme dissemos antes:
Agora vamos usar a definição do vetor de Poynting pra chegar a uma expressão para a densidade de energia, ok?
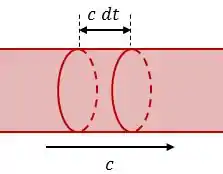
Substituindo na expressão de , teremos:
Finalmente, a densidade volumétrica média de energia do feixe será dada por:
Lembrando que . Portanto:
Resposta