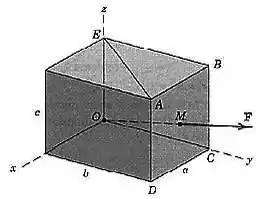
Se está no centro da face do sólido retangular, expresse como um vetor em termos dos vetores unitários . Determina a projeção escalar de ao longo da linha . Os valores de e são conhecidos.
Passo 1
Vamos definir a direção . O ponto é o ponto inicial e origem do sistema, assim:
Já está no centro de uma das faces. Pela figura:
Assim:
E o vetor unitário nessa direção é dado por:
Passo 2
Assim, a força é definida por:
Passo 3
Para achar a projeção da força na linha , vamos primeiro definir o vetor unitário que simboliza essa direção:
Passo 4
Então, a projeção será dada pelo produto escalar abaixo:
Efetuando o produto termo a termo, vamos ter que:
E qual a direção? :
Resposta
Exercícios de Livros Relacionados
Uma equipe de instalação de cabos quer estabelecer a dependência da força de tração T com a deflexão h do cabo. Faça um gráfico tanto da força trativa mínima T 0 quanto da força tativa T nos apoios A
Determine o ângulo theta entre a força de 200 N e a linha O C .
A mola com constante k = 2,6k N / m está presa ao disco no ponto A e à placa da extremidade no ponto B , como mostrado. A mola não está esticada quando θ A e θ B são, ambos, zero. Se o disco é girado
136. determine a intensidade da componente projetada da força de 500N que atua ao longo do eixo B C do tubo.
A força trativa no cabo de sustentação A B vale 10k N . Escreva, como um vetor T → , a força que o cabo exerce sobre a haste B C . Determine os ângulos θ x , θ y e θ z que a linha de ação de T → faz c