O tanque uniforme de é suspenso por meio de um cabo de de comprimento, que está preso às laterais do tanque e sobre a pequena polia localizada em Se o cabo pode ser preso nos pontos , determine qual amarração produz a menor quantidade de tração no cabo. Qual é esta tração?
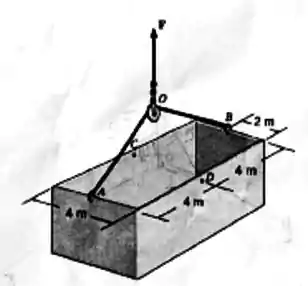
Passo 1
Primeiramente, veja que a força precisa equilibrar o peso. Assim, o módulo dela vai ser sempre igual a:
Aqui nós vamos usar a regra do paralelogramo, visto em tópicos anteriores, pra calcular a tensão nos fios.
Como as distribuições em são sempre simétricas, a força será a mesma em ambos os cabos:
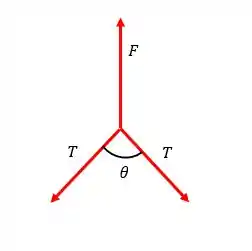
Então:
E o que vai mudar pra cada caso? O ângulo . Dessa forma, vamos conseguir analisar qual configuração gera o menor valor pra
Passo 2
Caso
O triângulo formado tem os seguintes ângulos:
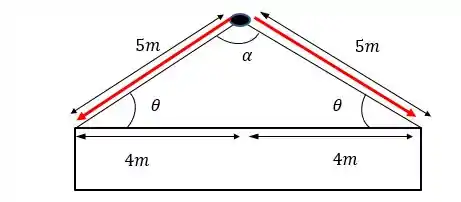
Por que a hipotenusa dos triângulos retângulos tem
Porque o enunciado disse que o cabo tem de comprimento, assim, cada metade dele tem que ter
Com essas informações, podemos calcular
E
Show de bola, agora é fácil achar
Passo 3
Para o caso , vamos fazer a mesma coisa, só que as dimensões são outras:
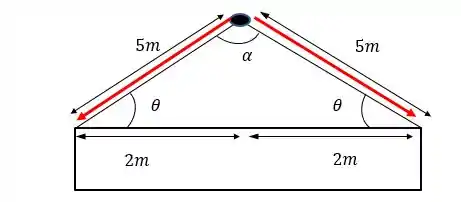
E:
Assim, a amarração em produz a menor tensão e ela vale: