Considere o sistema ilustrado na figura a seguir e determine os itens abaixo. (Use: e ).
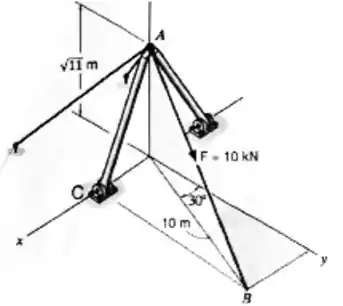
- Calcule o versor na direção e defina a força em notação vetorial cartesiana em termos deste versor.
- Calcule a intensidade da componente de ao longo da direção
Passo 1
Vamos calcular primeiro o ângulo que a força faz com o plano
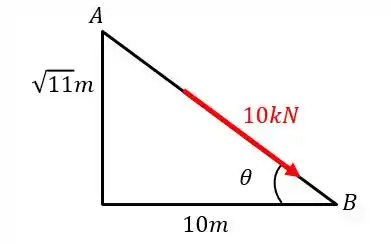
Então:
Assim:
Veja a figura de novo: se quisermos calcular a componente da força, primeiro temos que multiplicar por de modo a rebater a força para o plano e depois por para que ela fique no eixo .
Assim, a componente do versor é:
E a componente devemos multiplicar no final por
E a componente ? Apenas definida por:
E é negativa por que a força aponta para baixo!
E esse vetor já está normalizado? Sim e podemos comprovar isso calculando o seu módulo que deve dar como resposta:
Passo 2
Definindo a força em termos de
Passo 3
Basicamente, o item está te pedindo a projeção de em .
Pra isso, você tem que definir o vetor normal daquela direção. Então vamos trabalhar em cima do triângulo abaixo:
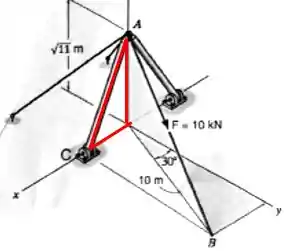
Perceba que a distância de até a origem é dada por:
Agora podemos calcular o ângulo que o versor faz com a horizontal:
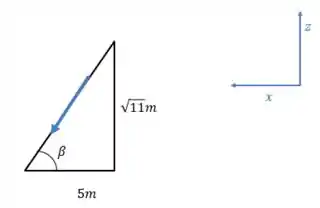
Assim:
Então:
Passo 4
Agora é só fazer: