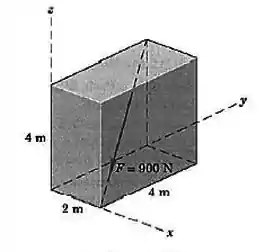
A força de módulo e atua ao longo da diagonal do paralelepípedo, como mostrado. Expresse em termos de seu módulo multiplicado pelo vetor unitário apropriado, e determine seus componentes e
Passo 1
O sentido da força já está mostrado na figura.
Vamos definir o ponto inicial e final que definem o vetor direção da força:
Sendo esse o ponto extremo da face superior do paralelepípedo.
E:
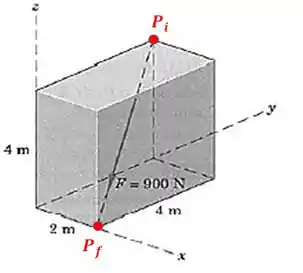
Assim, o vetor direção será dado por:
E o vetor normalizado:
Passo 2
Assim:
Portanto,
Resposta
Exercícios de Livros Relacionados
Uma equipe de instalação de cabos quer estabelecer a dependência da força de tração T com a deflexão h do cabo. Faça um gráfico tanto da força trativa mínima T 0 quanto da força tativa T nos apoios A
Determine o ângulo theta entre a força de 200 N e a linha O C .
A mola com constante k = 2,6k N / m está presa ao disco no ponto A e à placa da extremidade no ponto B , como mostrado. A mola não está esticada quando θ A e θ B são, ambos, zero. Se o disco é girado
136. determine a intensidade da componente projetada da força de 500N que atua ao longo do eixo B C do tubo.
A força trativa no cabo de sustentação A B vale 10k N . Escreva, como um vetor T → , a força que o cabo exerce sobre a haste B C . Determine os ângulos θ x , θ y e θ z que a linha de ação de T → faz c