Uma força é aplicada à superfície eda esfera como mostrado. Os ângulos localizam o ponto é o ponto médio de . Expresse de forma vetorial, usando as coordenadas dadas.
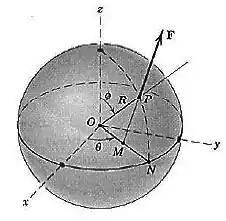
Dica:
Passo 1
Vamos primeiro analisar o plano , que faz um ângulo com :
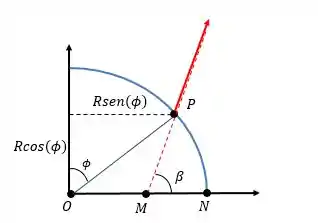
Nós temos que achar quanto vale o ângulo , pois ele é o ângulo que a linha de ação da força faz com a horizontal, conforme o desenho acima.
Beleza, mas como achar isso?
Perceba que existe um triângulo retângulo que possui um dos ângulos como sendo . Nesse triângulo, os catetos são:
E esse adjacente tá certo? Sim, perca que a projeção de na horizontal é , porém a força parte do ponto , que o ponto médio do segmento . Esse segmento, por sua vez, tem o comprimento do raio da esfera.
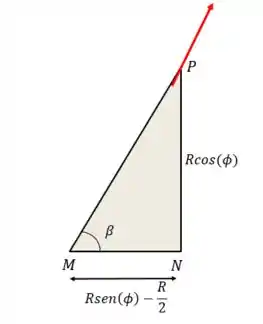
Então:
Agora usando:
Arrumando isso e tirando raiz quadrada nos dois lados:
E usando:
Com isso, temos o que precisamos para calcular as componentes da força.
Assim, no segmento , a força tem como componente horizontal:
E vertical:
Passo 2
Beleza, mas essas componentes foram calculadas no segmento . Queremos saber as componentes nos eixos
Dá uma olhada:
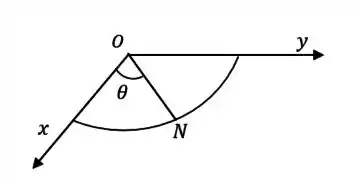
Então, a componente é dada por:
E continua sendo o
Passo 3
Então, a força pode ser escrita como: