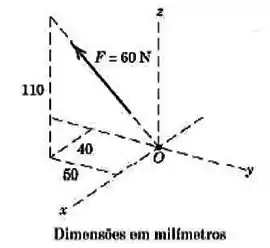
Expresse vetorialmente em termos dos vetores unitários e. Determine o ângulo entre e o eixo
Passo 1
Vamos primeiro definir o vetor da direção Sendo o ponto
E o ponto
Temos:
Normalizando-o:
Passo 2
Agora é só definir a força usando o vetor:
Efetuando as contas, chegamos a isso:
Passo 3
Nesse caso, achar o ângulo que a força faz com o eixo é mais simples do que em outros casos que iremos ver. Basta você usar um triângulo retângulo:
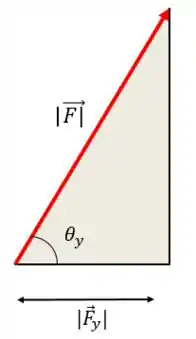
Lembrando que o módulo de vale
Mas como a componente da força na direção do eixo y tem sinal negativo, devemos considerar o suplemento desse ângulo. Ou seja: