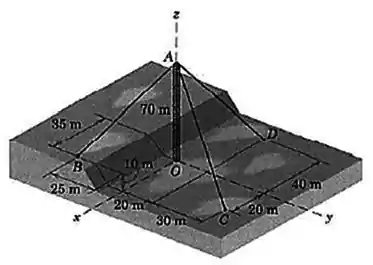
A torre de transmissão de micro-ondas com de altura é equilibrada por três cabos de amarração, como mostrado. O cabo suporta uma força trativa de . Expresse em forma vetorial a força correspondente no ponto
Passo 1
Nós devemos descobrir quem é o vetor que vai do ponto inicial para o ponto
Esta é uma força trativa, pois ela tem uma tendência de fazer os dois pontos se aproximarem.
Passo 2
Beleza, então como vamos achar o vetor normalizado Vamos primeiro gerar o vetor:
é o ponto final e o inicial. Depois vamos normalizá-lo.
Pela figura, da pra perceber que:
E :
Então:
Assim, normalizando:
Então, a força será dada por:
Resposta
Exercícios de Livros Relacionados
Uma equipe de instalação de cabos quer estabelecer a dependência da força de tração T com a deflexão h do cabo. Faça um gráfico tanto da força trativa mínima T 0 quanto da força tativa T nos apoios A
Determine o ângulo theta entre a força de 200 N e a linha O C .
A mola com constante k = 2,6k N / m está presa ao disco no ponto A e à placa da extremidade no ponto B , como mostrado. A mola não está esticada quando θ A e θ B são, ambos, zero. Se o disco é girado
136. determine a intensidade da componente projetada da força de 500N que atua ao longo do eixo B C do tubo.
A força trativa no cabo de sustentação A B vale 10k N . Escreva, como um vetor T → , a força que o cabo exerce sobre a haste B C . Determine os ângulos θ x , θ y e θ z que a linha de ação de T → faz c