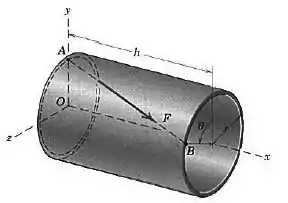
Uma força atua ao longo da linha dentro da casca cilíndrica circular, como mostrado. As quantidades são conhecidas. Usando as coordenadas mostradas, expresse como um vetor.
Passo 1
Essa é mais tranquila do que parece: primeiro vamos definir o vetor da direção
Depois, normalizando-o, vamos achar . Com esse vetor, vamos escrever a força como sendo:
Passo 2
O ponto pode ser definido por:
Dá pra ver pelo desenho?
No desenho não existe a sinalização de um ângulo e, além disso, o ponto está na face superior do cilindro. Assim, como o eixo é o eixo vertical, dá pra gente concluir que e as outras coordenadas são nulas.
E o ponto
Veja só: nesse caso, o raio faz um ângulo com a vertical. Além disso, ele está a uma distância da origem. Assim:
Passo 3
Então:
Bora calcular o vetor normalizado nessa direção, então?
Assim:
Passo 4
E por fim: