Universidade Federal de Pernambuco, Área II, Cálculo Numérico, 2019-2, 2ª prova, 15/10/2019, 4.
4. O código abaixo tem o objetivo de aplicar o método de interpolação de Lagrange para preencher o ponto f(3.7) a partir dos pontos destacados no código. Nesse contexto, preencha os espaços vazios corretamente.
Passo 1
Falaaaa, galera!! Neste exercício vamos desenvolver parte do algoritmo do método de interpolação de Lagrange. Ficou confuso? Vem comigo!
Esse método nos ajuda a determinar um polinômio que contém um conjunto de pontos tabelados. O enunciado já nos forneceu esses pontos, logo nas primeiras duas linhas do código. Temos , , e , onde e . Logo, o polinômio interpolador terá grau menor ou igual à 3, pois para pontos, sempre encontramos um polinômio de grau menor ou igual a .
Passo 2
Antes de entender o algoritmo, vamos relembrar o passo a passo do método de Lagrange. Basicamente temos um polinômio com essa cara:
e
Em que é o número de pontos tabelados, e . Lembrando que a contagem dos pontos começa em e por isso paramos em .
Passo 3
Nosso código vai ficar assim:
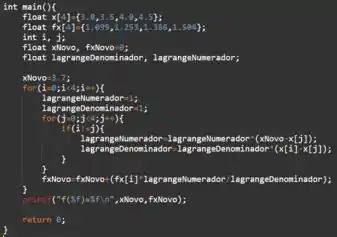
Nós começamos declarando todas as variáveis usadas no código. Já comentamos que os pontos tabelados (armazenados nos vetores x[4] e fx[4]), foram descritos na primeira e na segunda linha. Na terceira, temos i e j, variáveis auxiliares para os laços de repetição. Na quarta, temos o ponto que queremos preencher pelo polinômio interpolador, fornecido no enunciado! Ou seja, xNovo = 3.7 e fxNovo = P(3.7). E por fim, temos mais dois auxiliares que nos ajudarão a construir nosso polinômio, sendo que lagrangeNumerador conterá os fatores do numerador e lagrangeDenominador, do denominador.
O primeiro laço de repetição for roda para os valores , sendo que para cada rodada, iremos definir o "sub polinômio" Como estamos trabalhando com produtos, devemos inicializar lagrangeNumerador e lagrangeDenominador como valendo , que é o número neutro da multiplicação.
O segundo laço de repetição for roda para os valores mas desta vez estão associados diretamente aos valores de tabelados. O condicional if executa os dois comandos seguintes apenas para valores de diferentes de , pois como vimos na definição de anteriormente, não temos fatores dependendo de .
Em seguida, fazemos lagrangeNumerador = lagrangeNumerador * (xNovo - x[j]) e lagrangeDenominador = lagrangeDenominador * (x[i] - x[j]). Nestas linhas estamos definindo o numerador e o denominador de , para cada um dos valores de , como vimos na definição. Observe que já incluímos xNovo no cálculo, para obtermos fxNovo ao fim da execução do algoritmo.
Uma vez que o segundo laço executa suas quatro rodadas, uma para cada um dos pontos tabelados, podemos multiplicar o polinômio obtido por e somar este produto ao polinômio interpolador , que no nosso caso seria fxNovo.
Ao fim das quatro rodadas do primeiro laço, temos nosso polinômio interpolador e portanto o valor de fxNovo, que é impresso na última linha do código!
Tranquilo, galera?
Resposta
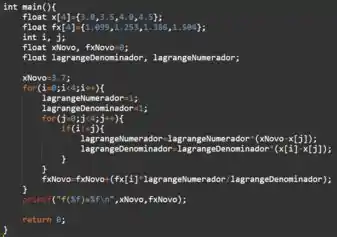
O algoritmo retorna: f(3.7) = 1.308384.