Considere a função
a) Encontre o domínio e a imagem de
b) O gráfico de é uma superfície quádrica? Se a resposta for sim, identifique a superfície e esboce gráfico de .
c) Indentifique as curvas de nível da função e esboce um mapa de contorno. Explique a relação entre o mapa de controno e o gráfico de
Passo 1
a) Nosso domínio será inciailamente garantir que o que está dentro da raiz seja positivo. Então temos:
Para imagem temos apenas
Passo 2
b) Só de olhar pra carinha da função da pra ver que ela é uma superfície quádrica sim! Ou seja, tem sua simetria entre seus eixos.
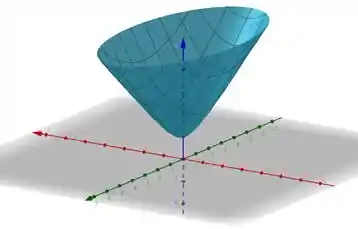
Aí você me pergunta, amigo, mas como eu saio disso pra essa imagem aí? Simples!
Opa, olha como isso tem a carinha de um hiperboloide, o detalhe é esse +1 que desloca a função pra z positivo, formando então um hiperbolóde de duas folhas! No caso, estamos trabalhando com o lado positivo.
Passo 3
c) agora sobre as curvas de nível, para identificalas, vamos fixar um C qualquer:
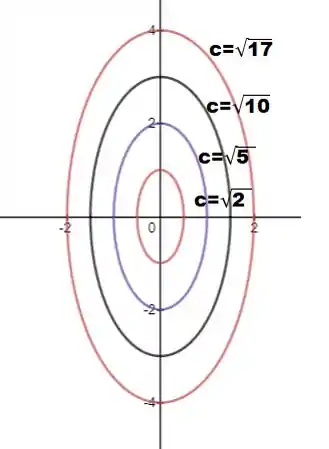
Opa, isso faz com que a gente perceba que as curvas de nível serão elipses conforme o varia.
Queremos agora montar o mapa de contorno com alguns C que facilitem nossa vida pra desenhar. Ou seja, , onde
Vou escolher como esse snpumeros quadrados 1, 4, 9 e 16 para desenhar 4 curvas.
Assim temos:
Eis então o esboço.
Resposta
Ei, a resposta está no passo a passo :)