PUC-RIO – Cálculo 3 – 2020.2 – G1 (Parte 2) – Discursiva
Considere o paraboloide
e o plano
(1.0) Determine a equação da projeção no plano da curva interseção do paraboloide com o plano e faça um esboço desta curva.
(1.0) Encontre uma parametrização da curva interseção de com .
Passo 1
O ponta pé inicial para a gente resolver esse exercício é descobrir a curva da interseção pois é isso que o item nos pede e para resolver o item precisamos dela e vamos conseguir ela igualando a equação do paraboloide com o plano e mexendo um pouquinho nela.
Ainda tá com dúvida? Vamos resolver tudo bonitinho então pra você!
Passo 2
Como falei no item anterior vamos igualar as duas equações:
Completando quadrado:
A projeção da curva de interseção no plano é um círculo com centro e raio .
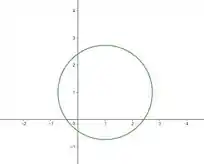
Passo 3
Agora só nos resta fazer a parametrização do círculo que encontramos no item anterior.
Sabemos que:
Sendo assim:
,
Resposta
,