Identifique que a Quádrica na forma quadrática abaixo
Passo 1
Primeiramente, observamos que essa não é uma quádrica do jeito que estamos acostumados. Os termos de potência 1 e os produtos mistos nos levam a pensar que ela está com o centro deslocado e rotacionada.
Vamos escrever a sua equação na forma matricial:
Passo 2
A partir da matriz , encontramos seus autovalores.
Para calcular os autovalores de uma matriz 3x3:
Devemos fazer:
Isso implica:
No nosso caso:
Então temos:
Calculando o determinante caímos no polinômio característico:
Vamos tentar encontrar uma raiz testando os primeiros valores dos divisores de 162.
Por exemplo, vamos testar 2 e 3. Substituindo na equação verificamos que 3 é uma raiz. Portanto:
Agora vamos usar o método de briot-ruffini para diminuir um grau na equação. Funciona assim:
A primeira coisa a fazer é escrever essa equação completa, colocando vezes o elevado aos graus que não aparecem (já está nessa forma):
Agora montamos o seguinte quadrinho:

No canto superior esquerdo colocamos os coeficientes da nossa equação, no canto superior direito colocamos o valor na nossa raiz .
Agora nós fazemos os seguintes passos. Primeiro descemos o primeiro coeficiente, que vai ficar:

O próximo passo é multiplicar esse número que baixamos pelo número ali no canto superior direito, e depois somar com o próximo coeficiente.
Nesse caso fazemos
Esse nessa equação imediatamente acima é o coeficiente, o 3 é o número do canto superior direito e aquele outro é o próximo coeficiente.
Fazendo essa conta chegamos ao valor , colocamos esse valor embaixo do coeficiente , ficando:

Agora é só repetir, a nossa conta dessa vez vai ficar:
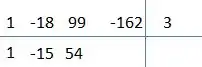
Agora é só repetir, a nossa conta dessa vez vai ficar:

Como aquele último cara deu a nossa conta está certinha, se não der alguma conta está errada.
A nossa nova equação vai ser aquela que tem os coeficientes de baixo, tirando aquele , começando com um grau a menos do que o anterior, neste caso vamos ter:
Resolvendo encontramos:
Então temos:
Passo 3
Precisamos encontrar os autovetores unitários.
Vamos calcular o autovetor referente a . Para isso faremos:
Temos:
Então:
Da primeira equação:
Da terceira equação temos:
Fica:
Arbitrando valores para temos:
Achando o autovetor unitário temos:
Passo 4
Calculando agora o autovetor referente a faremos:
Temos:
Então:
Da primeira equação:
Da terceira equação:
Fica:
Arbitrando valores para temos:
Achando o autovetor unitário temos:
Passo 5
Calculando agora o autovetor referente a faremos:
Temos:
Então:
Da primeira equação:
Da terceira:
Fica:
Arbitrando valores para temos:
Achando o autovetor unitário temos:
Passo 6
Agora que calculamos os autovalores e autovetores, podemos jogar os valores encontrados na equação matricial:
Fica:
Fazendo essa multiplicação matricial chegamos em:
Que é a equação de um elipsoide.
Resposta
A quádrica é um elipsoide.