Um escoamento incompressível bidimensional é dado pelo campo de velocidade , em unidades arbitrárias. Esse escoamento satisfaz a continuidade? Em caso afirmativo, encontre a função corrente e faça um gráfico de algumas linhas de corrente, com setas.
Passo 1
Como ele já nos deu o campo de velocidades, a gente tem que
Passo 2
Para ver se esse escoamento satisfaz a equação da continuidade, devemos ver se satisfazem a seguinte equação
Passo 3
Pelas expressões do passo 1, temos que
Então temos que
Logo o escoamento satisfaz a equação da continuidade
Passo 4
A definição da função corrente é
Então temos que seguir o passo a passo abaixo
Passo 5
Escolha uma das duas equações para integrar
Por conveniência, vou integrar a equação do , ou seja
Essa função surgiu porque qualquer coisa que dependesse só de foi tratada como constante ao fazer a derivada parcial com respeito a .
Passo 6
Derivamos a expressão obtida no passo anterior com relação a outra variável, ou seja, devemos calcular:
Fazendo as continhas, temos
Passo 7
Pela definição da função corrente, temos que
Integrando a equação acima, temos
Passo 8
Assim, juntando tudo temos que
Passo 9
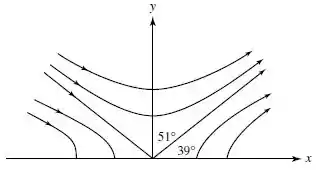
Colocando os valores de , temos hipérboles como na figura abaixo!
Resposta
Satisfaz a equação da continuidade!