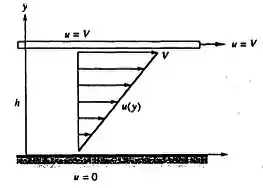
Mostre que o escoamento de Couette linear entre placas na Figura tem uma função corrente, mas não tem potencial de velocidade. Qual é a razão disso?
Passo 1
A primeira coisa que temos que achar são as componentes do vetor velocidade. A componente é simples de achar, porque o próprio desenho nos mostra
A componente varia linearmente, lá no gráfico o perfil é uma reta, de 0 na posição até na posição , então pela equação da reta a gente tem que
Passo 2
Para saber se existe função corrente, temos que ver se a equação da continuidade é satisfeita, então vamos lá
Então ,temos que
Logo, o escoamento satisfaz a equação da continuidade e a função corrente existe.
Passo 3
Para descobrir qual é a função corrente a gente segue o mesmo passo a passo, vamos integrar a expressão de primeiro:
Derivando com relação a a expressão de que a gente acabou de achar, temos
Comparando com a componente , temos
Logo, a função corrente é da forma
Passo 4
Para verificar se a função potencial existe, devemos ver se o escoamento é irrotacional. Como o escoamento tem apenas duas componentes de velocidade a gente tem que verificar essa igualdade aqui:
Passo 5
Fazendo as contas a gente tem que
Assim, a gente tem que
Logo o escoamento é rotacional e não admite função potencial!
Resposta
Não existe função potencial!