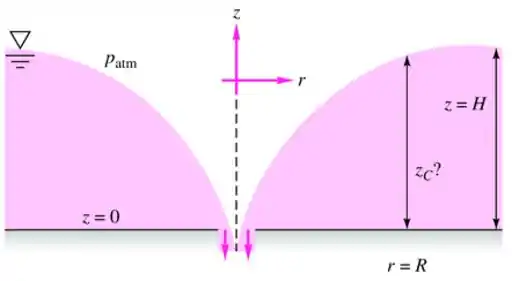
Um líquido é drenado por um pequeno furo em um tanque, como mostra a Figura, de forma que o campo de velocidade é dado por , , , em que é a profundidade da água distante do furo. Esse padrão de escoamento é rotacional ou irrotacional? Encontre a profundidade da água no raio .
Passo 1
Primeiro temos que ver se o escoamento é irrotacional. Vou te dar outra expressão que vai facilitar a sua vida quando tiver trabalhando com coordenadas polares! Para ver se um escoamento em coordenadas polares é irrotacional, a gente tem que verificar essa equação:
Passo 2
Pelo enunciado a gente sabe que
Como é uma constante, o primeiro termo da equação do passo 1 é zero. Como não depende de o segundo termo da equação também é zero, logo o escoamento é irrotacional.
Passo 3
Cara, quando a gente vê esses exercícios com altura e pressão a gente fica com uma vontade de tacar Bernoulli né não?
Então, a gente tem que tomar cuidado, porque a gente só pode fazer isso com uma série de hipóteses sendo satisfeitas e numa mesma linha de corrente.
Sabe uma parte ótima dos escoamentos irrotacionais? A equação de Bernoulli é válida sempre nesses escoamentos!
Show, então podemos escrever o seguinte:
Passo 4
Agora, precisamos entender que são alguns desses termos aí! Pô, a única componente do vetor velocidade que não é nula é , então o módulo da velocidade é igual a essa componente. Assim,
Fazendo o limite quando a gente acha o termo que é
Passo 5
Substituindo esses valores na equação de Bernoulli, a gente acha que
Resposta
O escoamento é irrotacional