P1 de Álgebra Linear I - MAT1200 da PUCRIO - 2016.2

Decida se cada afirmação abaixo é verdadeira ou falsa. Se a afirmação for verdadeira, apresente uma demonstração. Se a afirmativa for falsa, exiba um contraexemplo.

1. Se o conjunto de vetores é linearmente dependente, então o subconjunto { é linearmente dependente.
2. Se então o conjunto é linearmente dependente

Decida se cada afirmação abaixo é verdadeira ou falsa. Se a afirmação for verdadeira, apresente uma demonstração. Se a afirmativa for falsa, exiba um contraexemplo.

c) Se e são vetores não nulos e com a mesma direção, então

d) Se e são vetores do ortogonais e de mesmo módulo, então

Considere as retas e de dadas pelas equações e respectivamente. Considere uma circunferência de centro e raio inscrita entre as duas retas como na figura abaixo.

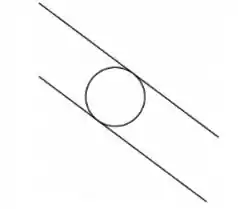
1. Determine todos os pontos que equidistam das retas e
2. Determine o valor de
3. Determine a equação da reta que passa por e é ortogonal às retas e
4. Determine o valor do raio
5. Assuma que o segumento de reta é a projeção ortogonal de em e determine as coordenadas de e de

Considere as retas:

Determine:

1. A distância entre as retas e .
2. A equação cartesiana do plano que contém e é paralelo a
3. Uma equação paramétrica da reta que é a reflexão de com relação ao plano definido no item (b)