Considere as retas e de dadas pelas equações e respectivamente. Considere uma circunferência de centro e raio inscrita entre as duas retas como na figura abaixo.
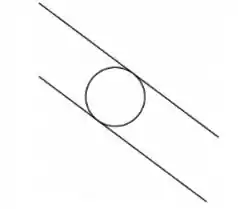
- Determine todos os pontos que equidistam das retas e
- Determine o valor de
- Determine a equação da reta que passa por e é ortogonal às retas e
- Determine o valor do raio
- Assuma que o segumento de reta é a projeção ortogonal de em e determine as coordenadas de e de
Passo 1
- Determine todos os pontos que equidistam das retas e
Esses pontos vão ser pertencentes a uma terceira reta, paralela as duas, que corta o meio da circunferência.
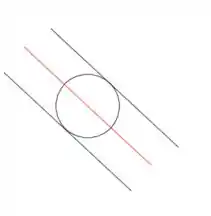
Os coeficientes das variáveis da equação vão ser iguais aos das outras retas, já que o vetor normal de retas paralelas é sempre o mesmo. Assim, meu conjunto de pontos tem essa cara:
Agora precisamos de um ponto para achar Podemos achar um ponto de uma reta e um ponto da outra e calcular o meio desses pontos. Como deve ser equidistante, obrigatoriamente esse ponto deve estar na reta que buscamos!
e
O meio desses pontos pode ser achado fazendo:
Substituindo na equação, temos que:
Passo 2
b)
Vamos, agora, achar o ponto Sabemos que ele está na reta que achamos na letra a) e que tem as coordenadas iguais como nos disseram no enunciado, .
Então, temos com :
Passo 3
c)
A reta que queremos é essa daqui:
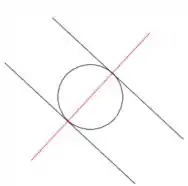
O vetor diretor dessa reta é o vetor normal das retas e que já conhecemos: .
Além disso, temos que essa reta passa pelo ponto Com um vetor diretor e um ponto, conseguimos achar a equação paramétrica:
Agora é só tranformar isso em equação cartesiana:
Temos então que:
Passo 4
d)
Conseguimos ver que o raio ta na reta que achamos na letra c)
Podemos achar o ponto o ponto em que a reta perpendicular achada em c) cruza a reta e calcular a sua distância até a o ponto :
Como o ponto pertence à duas retas posso igualar as equações para achar suas coordenadas:
Então e
O raio sera o módulo desse vetor:
Passo 5
e)
Vou chamar de o ponto na reta que cruza com a paralela mais a esquerda da reta e de o ponto da reta que cruza com a paralela mais a direita da reta
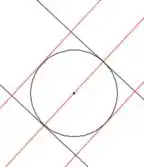
Bom, já temos o , o e o . Assim, conseguimos calcular e , utilizando, simplesmente no fato que eles são ortogonais! Trocando as coordenadas de lugar e mudando o sinal de uma delas:
e
Repare que eu escolhi o sinal olhando para a imagem e vendo o que fazia sentido, por exemplo, como está apontando para baixo, sua coordenada deve ser negativa!
Assim conseguimos encontrar os pontos pedidos usando o fato de que um vetor é o ponto da extremidade menos o ponto da origem:
Resposta
a)
b)
c)
d)
e) e