Considere as retas:
Determine:
- A distância entre as retas e .
- A equação cartesiana do plano que contém e é paralelo a
- Uma equação paramétrica da reta que é a reflexão de com relação ao plano definido no item (b)
Passo 1
a)
Para calcular a distância entre retas precisamos ligá-las por uma reta que seja perpendicular às duas:
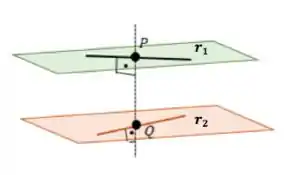
E medir o tamanho, ou seja, o módulo do vetor . Sabemos que:
- sua origem é um ponto de e sua extremidade é um ponto de
- ele é ortogonal ao vetor diretor de e ao vetor de , ou seja, e
Vamos aplicar isso aí então, primeiro achamos o vetor genérico :
Agora vamos fazer o produto interno desse vetor com os vetores diretores de cada reta:
Agora é só resolver o sistema:
E assim achamos e
Substituindo, vamos achar nosso vetor:
Pra terminar, agora, é só calcular o seu módulo:
Passo 2
b)
Para encontrarmos a equação cartesiana de um plano precisamos de 2 informações:
- ponto pertencente ao plano
- vetor normal ao plano
Como a reta pertence ao plano que quero criar, posso escolher um ponto dela como o meu ponto. Por exemplo, .
O meu vetor normal precisa ser ortogonal tanto ao vetor diretor de como ao de . Assim, aplicamos o produto vetorial:
Como as coordenadas do vetor normal são os coeficientes das variáveis da equação do plano, temos:
E agora usamos o ponto para achar
Assim,
Passo 3
c)
Como sabemos da letra b, a reta é paralela ao plano, ou seja, ela não corta o plano!
Assim, a reflexão vai ser simplesmente ver qual a reta é paralela ao plano e está a mesma distancia dele que a reta está.
Repara que essa distancia é a mesma distância que calculamos na letra a.
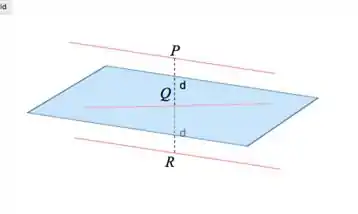
![]()
Substituindo os valores que já temos:
Sendo que então:
Temos o ponto, e o vetor diretor vai ser o mesmo de , então: