Considere o plano em que passa pela origem de equação cartesiana
e a transformação linear espelhamento (ou reflexão) em relação ao plano Denote por a matriz de E na base canônica.
(d) Seja B uma matriz ortogonalmente diagonalizável. Mostre que Para isso lembre da forma
(e) Considere uma transformação linear que tem uma base ortonormal de autovetores e determinante 0. Seja:
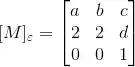
A matriz de M na base canônica. Determine os valores de a,b,c e d.
Passo 1
(d) Se B é ortogonalmente diagonalizável, então podemos escrever:
Com D diagonal e Q ortogonal.
Transpondo os dois lados dessa igualdade:
Usando a fórmula de transposta do produto dada no enunciado:
Mas:
Então:
Passo 2
(e) Vimos no item anterior que se M tem uma base ortonormal de autovetores, significa que M é ortogonalmente diagonalizável e portanto simétrica.
Ou seja:
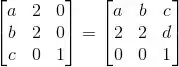
Daí achamos os valores:
Para achar a, vamos usar que o determinante de M é 0.
Calculando esse cara:
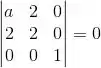
Resposta
(d) Demonstração.
(e) ,